Tìm điểm cố định mà mỗi đường thẳng d’ y = (m – 2)x + 3

Tìm điểm cố định mà mỗi đường thẳng d’: y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Giải sách bài tập Toán 8 Bài tập cuối chương 5 - Chân trời sáng tạo

Bài 17 trang 19 sách bài tập Toán 8 Tập 2: Tìm điểm cố định mà mỗi đường thẳng d’: y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Lời giải:

Giả sử điểm cố định của đồ thị hàm số y = (m – 2)x + 3 là I(x₀; y₀).

Thay x = x₀và y = y₀ vào y = (m – 2)x + 3, ta được:

y₀ = (m – 2)x₀ + 3

$\Leftrightarrow$ mx₀– 2x₀+ 3 – y₀= 0

$\Leftrightarrow$ mx₀ – (y₀ + 2x₀ – 3) = 0 (1)

Để (1) luôn đúng với mọi giá trị của m thì 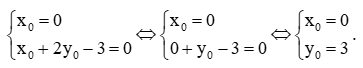Tìm điểm cố định mà mỗi đường thẳng d’ y = (m – 2)x + 3 .

Vậy đồ thị hàm số y = (m – 2)x + 3 luôn đi qua điểm cố định I(0; 3).

Lời giải SBT Toán 8 Bài tập cuối chương 5 hay khác: