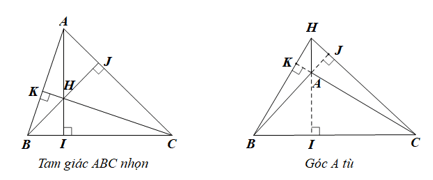
Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC

Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC. Dùng công thức tính diện tích tam giác để chứng minh:

Giải sách bài tập Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.29 trang 44 sách bài tập Toán 8 Tập 1: Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC. Dùng công thức tính diện tích tam giác để chứng minh:

$\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=1.$

Hỏi khi góc A của tam giác ABC là góc tù thì công thức đó thay đổi thế nào?

Lời giải:

Kí hiệu S là diện tích tam giác.

• Xét trường hợp tam giác ABC nhọn, ta có

$S_{HBC}=\frac{1}{2}\cdot HI\cdot BC;$ $S_{ABC}=\frac{1}{2}\cdot AI\cdot BC$

Suy ra $\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{1}{2}\cdot HI\cdot BC}{\frac{1}{2}\cdot AI\cdot BC}=\frac{HI}{AI}$

Chứng minh tương tự, ta có: $\frac{S_{HAC}}{S_{ABC}}=\frac{HJ}{BJ}$ và $\frac{S_{HAB}}{S_{ABC}}=\frac{HK}{CK}$.

Suy ra, $\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}$(do H nằm bên trong tam giác ABC)

Do đó $\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=\frac{S_{ABC}}{S_{ABC}}=1$.

• Khi góc A là góc tù, H nằm trong góc đối đỉnh với góc BAC, ta có

S_ABC = S_HBC – S_HAB – S_HAC nên ta được $1=\frac{HI}{AI}-\frac{HJ}{BJ}-\frac{HK}{CK}$.

Lời giải SBT Toán 8 Bài tập cuối chương 3 hay khác:

• Câu 1 trang 43 sách bài tập Toán 8 Tập 1: Trong các câu sau, câu nào đúng? ...

• Câu 2 trang 43 sách bài tập Toán 8 Tập 1: Trong các câu sau, câu nào đúng? ...

• Câu 3 trang 43 sách bài tập Toán 8 Tập 1: Tìm câu sai trong các câu sau: ...

• Câu 4 trang 43 sách bài tập Toán 8 Tập 1: Cho các câu sau: Tứ giác mà hai góc kề một cạnh tuỳ ý của nó là hai góc bù nhau là một hình bình hành ...

• Bài 3.28 trang 44 sách bài tập Toán 8 Tập 1: Cho tam giác ABC. Với mỗi điểm M nằm giữa B và C, lấy điểm N thuộc cạnh AB ...

• Bài 3.30 trang 44 sách bài tập Toán 8 Tập 1: Khái niệm tam giác, tứ giác có thể mở rộng thành khái niệm n − giác (n là số tự nhiên lớn hơn 2) như sau ...

• Bài 3.31 trang 44 sách bài tập Toán 8 Tập 1: Hai cạnh kề nhau của một n – giác là hai cạnh có cùng chung một đỉnh của n – giác đó ...

• Bài 3.32 trang 44 sách bài tập Toán 8 Tập 1: n – giác gọi là n – giác đều nếu tất cả các cạnh của nó bằng nhau và tất cả các góc của nó bằng nhau ...