Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng

Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng - Kết nối tri thức

Bài 4.20 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng $\frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}$

 (HD. Ta có sin B = $\frac{AH}{AB}$, sin C = $\frac{AH}{AC}$, cos B = sin C và áp dụng công thức sin² α + cos² α = 1 với mọi góc nhọn α).

Lời giải:

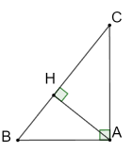
Xét tam giác ABH vuông tại H, ta có: $\tan \widehat{ABH}=\frac{AH}{BH}$

Xét tam giác ACH vuông tại H ta có: $\tan \widehat{ACH}=\frac{AH}{HC}$

Vì $\widehat{ABH}$ và $\widehat{ACH}$ là hai góc phụ nhau (tam giác ABC vuông tại A) nên:

$\tan \widehat{ABH}=\cot \widehat{ACH}=\frac{1}{\tan \widehat{ACH}}$ hay $\frac{AH}{BH}=\frac{HC}{AH}$

Suy ra AH² = BH . CH (đpcm).

Lời giải SBT Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay khác:

• Bài 4.18 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC. ...

• Bài 4.19 trang 49 sách bài tập Toán 9 Tập 1: Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \widehat{ABH}$ và $\tan \widehat{CAH}$ , suy ra AH² = BH . CH ...

• Bài 4.21 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có BC = 11 cm, $\widehat{ABC}=38°,\widehat{ACB}=30°.$ Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH. ...

• Bài 4.22 trang 49 sách bài tập Toán 9 Tập 1: Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba): ...

• Bài 4.23 trang 49 sách bài tập Toán 9 Tập 1: Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p > n và $\widehat{MPA}=\alpha$ (H.4.12) ...

• Bài 4.24 trang 49 sách bài tập Toán 9 Tập 1: Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn 15° ...

• Bài 4.25 trang 50 sách bài tập Toán 9 Tập 1: Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2 km, nhìn thấy chiếc tàu C ở phía xa với với $\widehat{CAB}=50°,\widehat{CBA}=45°$ ...

• Bài 4.26 trang 50 sách bài tập Toán 9 Tập 1: Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m ...

• Bài 4.27 trang 50 sách bài tập Toán 9 Tập 1: Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° ...