Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p lớn hơn n

Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p > n và (H.4.12). Chứng minh rằng: .

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng - Kết nối tri thức

Bài 4.23 trang 49 sách bài tập Toán 9 Tập 1: Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p > n và $\widehat{MPA}=\alpha$ (H.4.12). Chứng minh rằng: $AB=\frac{p\tan \alpha -n}{\sin \alpha }$.

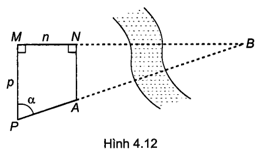
Lời giải:

Vì AN và PM cùng vuông góc với MN nên AN // PM.

Vì AN // PM nên $\widehat{BAN}=\widehat{BPM}=\alpha$

+ Xét tam giác BAN vuông tại N ta có:

$BN=AB\sin \widehat{BAN}=AB.\sin \alpha$

+ Xét tam giác BPM vuông tại M ta có:

$BM=PM.\tan \widehat{BPM}=p.\tan \alpha$

Ta có: BM – BN = MN

p . tan α – AB . sinα = n

AB . sinα = p . tanα – n

$AB=\frac{p.\tan \alpha -n}{\sin \alpha }$ (đpcm).

Lời giải SBT Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay khác:

• Bài 4.18 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC. ...

• Bài 4.19 trang 49 sách bài tập Toán 9 Tập 1: Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \widehat{ABH}$ và $\tan \widehat{CAH}$ , suy ra AH² = BH . CH ...

• Bài 4.20 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng $\frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}$ ...

• Bài 4.21 trang 49 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có BC = 11 cm, $\widehat{ABC}=38°,\widehat{ACB}=30°.$ Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH. ...

• Bài 4.22 trang 49 sách bài tập Toán 9 Tập 1: Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba): ...

• Bài 4.24 trang 49 sách bài tập Toán 9 Tập 1: Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn 15° ...

• Bài 4.25 trang 50 sách bài tập Toán 9 Tập 1: Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2 km, nhìn thấy chiếc tàu C ở phía xa với với $\widehat{CAB}=50°,\widehat{CBA}=45°$ ...

• Bài 4.26 trang 50 sách bài tập Toán 9 Tập 1: Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m ...

• Bài 4.27 trang 50 sách bài tập Toán 9 Tập 1: Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° ...