Trên bờ của một cái ao cá hình tròn, người ta dựng ba cái chòi câu cá tại các điểm A, B và C
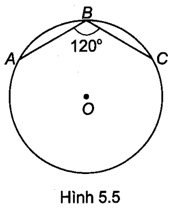
Trên bờ của một cái ao cá hình tròn, người ta dựng ba cái chòi câu cá tại các điểm A, B và C. Biết rằng tam giác ABC cân tại B và có AB = BC = 10 m, = 120° (H.5.5).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên - Kết nối tri thức
Bài 5.13 trang 62 sách bài tập Toán 9 Tập 1: Trên bờ của một cái ao cá hình tròn, người ta dựng ba cái chòi câu cá tại các điểm A, B và C. Biết rằng tam giác ABC cân tại B và có AB = BC = 10 m, = 120° (H.5.5).
a) Tính bán kính của ao cá.
b) Tính độ dài quãng đường (men theo bờ ao) từ chòi A đến chòi B và chòi C (làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải:
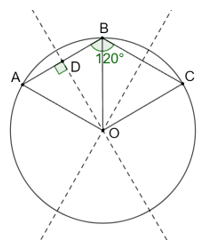
Gọi O là tâm cái ao. Do đó OA = OC, suy ra O nằm trên đường trung trực của AC.
Mà tam giác ABC cân tại B nên đường trung trực của AC đồng thời là đường phân giác của góc ABC, do đó:
Do OA = OB (bán kính đường tròn (O)) mà nên tam giác OAB là tam giác đều, suy ra OA = AB = 10 cm.
Vậy bán kính ao cá là 10 cm.
b) Độ dài quãng đường từ A đến B là độ dài cung nhỏ AB và có giá trị bằng:
(m)
Ta thấy AB = BC = AO = OC = 10 cm nên ABCO là hình thoi.
Suy ra BO là đường phân giác của góc AOC.
Do đó độ dài cung nhỏ AB bằng độ dài cung nhỏ BC.
Suy ra quãng đường từ A đến C bằng 2 lần độ dài cung nhỏ AB và bằng:
(m).
Vậy quãng đường từ A đến B dài xấp xỉ 10,8 m và quãng đường từ A đến C dài xấp xỉ 20,9 m.
Lời giải SBT Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên hay khác: