Giải Tin học 11 trang 130 Cánh diều
Haylamdo biên soạn và sưu tầm với Giải Tin học 11 trang 130 trong Bài 9: Lập trình sắp xếp nhanh Tin học lớp 11 Cánh diều hay nhất, ngắn gọn sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Tin 11 trang 130.
Giải Tin học 11 trang 130 Cánh diều
Nhiệm vụ 1 trang 130 Tin học 11: Viết chương trình thực hiện sắp xếp nhanh một dãy số và chạy thử kiểm tra.
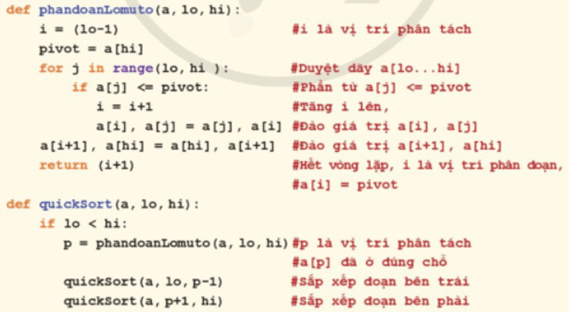
a) Dựa trên mã lệnh thuật toán cho trong Hình 3.
b) Dựa trên mã lệnh thuật toán cho trong Hình 5.
Lời giải:
a. Dựa trên mã lệnh thuật toán cho trong Hình 3.
b) Dựa trên mã lệnh thuật toán cho trong Hình 5.
Nhiệm vụ 2 trang 130 Tin học 11: Bổ sung thêm các câu lệnh in kết quả trung gian vào các chương trình nói trên để có thể quan sát diễn biến từng bước thực hiện sắp xếp nhanh một dãy số.
Lời giải:
Câu lệnh in ra màn hình: print(".....")
Các bước thực hiện
Phân tích bài toán
Độ phức tạp thuật toán:
Vận dụng trang 130 Tin học 11: Em hãy thực hiện các công việc sau:
a) Sửa lại thủ tục phân đoạn đề có hàm quickSort_ down sắp xếp theo thứ tự giảm dần.
Gợi ý. Sửa đối phép so sánh trong câu lệnh 1f a[3] <= pivot: thành 1f a[3]} >= pivot:
b) Tiếp tục sửa lại để có hàm quickSort_tuple down sắp xếp danh sách các cặp. ví dụ (tên học sinh, điểm môn học) theo điệm môn học giảm dần.
Gợi ý: Sửa đổi đầu vào thành danh sách các cặp (tên học sinh, điểm môn học) và thực hiện so sánh theo điểm môn học.
Lời giải:
a)Gợi ý
void swap(int *a,int *b){
int temp=*a;
*a=*b;
*b=temp;
}
void bubblesort(int arr[],int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(arr[j]>arr[j+1]){
swap(&arr[j],&arr[j+1]);
}
}
}
}
b) Gợi ý
void quickSort(int a[], int l, int r){
int p = a[(l+r)/2];
int i = l, j = r;
while (i < j){
while (a[i] < p){
i++;
}
while (a[j] > p){
j--;
}
if (i <= j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
i++;
j--;
}
}
if (i < r){
quickSort(a, i, r);
}
if (l < j){
quickSort(a, l, j);
}
}
Câu 1 trang 130 Tin học 11: Em hãy giải thích tại sao lại nói thuật toán sắp xếp nhanh (QuickSort) theo chiến lược “chia đề trị”.
Lời giải:
Thuật toán QuickSort được xây dựng theo chiến lược "chia để trị" bởi vì nó phân chia dãy số cần sắp xếp thành các phần nhỏ hơn, sau đó sắp xếp từng phần đó và kết hợp các phần đã sắp xếp lại thành dãy số đã được sắp xếp.
Cụ thể, thuật toán QuickSort chia dãy số cần sắp xếp thành hai phần dựa trên một phần tử được gọi là pivot. Tất cả các phần tử nhỏ hơn pivot được đưa về bên trái pivot, còn các phần tử lớn hơn pivot được đưa về bên phải pivot. Sau đó, thuật toán đệ quy được áp dụng lên từng phần của dãy số này, cho đến khi các phần con chỉ còn duy nhất một phần tử. Cuối cùng, các phần đã sắp xếp lại với nhau để tạo ra dãy số đã được sắp xếp.
Vì vậy, chiến lược "chia để trị" của QuickSort cho phép thuật toán chia nhỏ vấn đề lớn hơn thành các vấn đề nhỏ hơn, giúp cho việc giải quyết các vấn đề này trở nên đơn giản và hiệu quả hơn."
Câu 2 trang 130 Tin học 11: Theo em thì diễn biến từng bước sắp xếp nhanh một dãy số cụ thể dùng phân đoạn Lomuto sẽ giống hay sẽ khác với dùng phân đoạn Hoare?
Lời giải:
Diễn biến từng bước sắp xếp nhanh một dãy số cụ thể dùng phân đoạn Lomuto sẽ khác với dùng phân đoạn Hoare. Sự khác biệt giữa phương pháp phân đoạn Lomuto và phân đoạn Hoare trong thuật toán QuickSort là ở việc chọn pivot, cách phân đoạn và cách sắp xếp các phần tử.
Cụ thể, phương pháp phân đoạn Lomuto sẽ chọn pivot là phần tử cuối cùng của mảng, phân đoạn theo pivot và sau đó đưa pivot về giữa hai phân đoạn, tiếp tục thực hiện thuật toán QuickSort trên hai phân đoạn trái và phải của pivot. Trong khi đó, phương pháp phân đoạn Hoare sẽ chọn pivot là phần tử ở giữa mảng, đưa hai con trỏ từ đầu và cuối mảng trỏ tới nhau và dịch chuyển chúng sao cho phần tử bên trái pivot lớn hơn pivot, phần tử bên phải pivot nhỏ hơn pivot, sau đó đưa pivot về vị trí mới và thực hiện QuickSort trên hai phân đoạn trái và phải của pivot.