Giải Tin học 12 trang 161 Cánh diều (Khoa học máy tính)

Haylamdo biên soạn và sưu tầm lời giải bài tập Tin học 12 trang 161 trong Bài 2: Thực hành về mô phỏng Tin 12 Cánh diều hay nhất, ngắn gọn sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Tin 12 trang 161.

Giải Tin học 12 trang 161 Cánh diều (Khoa học máy tính)

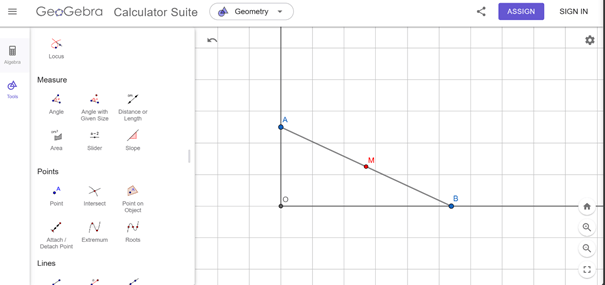
Vận dụng 1 trang 161 Tin học 12: Cho góc vuông xOy với điểm O cố định, điểm A cố định trên Oy, khi điểm B di chuyển trên Ox thì điểm M là trung điểm của AB di chuyển ra sao

Lời giải:

Khi điểm B di chuyển trên trục Ox, điểm M sẽ là trung điểm của đoạn thẳng AB. Để mô tả di chuyển của điểm M, chúng ta có thể sử dụng hệ tọa độ.

Gọi tọa độ của điểm A là (0;y_A) là tọa độ của điểm A trên trục Oy.

Gọi tọa độ của điểm B là (x_B;0) là tọa độ của điểm B trên trục Ox.

Do M là trung điểm của AB, ta có:

Tọa độ của điểm M là

Khi B di chuyển trên trục Ox, tọa độ của điểm B thay đổi, do đó tọa độ của M cũng thay đổi tương ứng theo công thức trên.

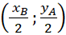
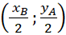
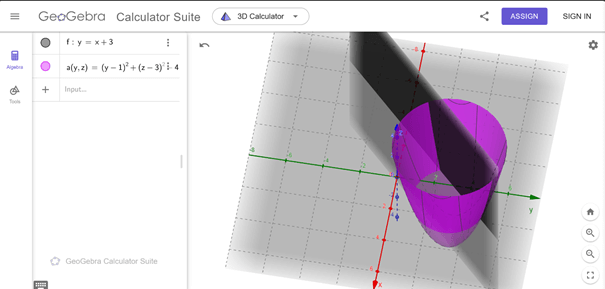
Tóm lại, khi B di chuyển trên trục Ox, M di chuyển sao cho tọa độ của M thay đổi theo công thức , tức là tọa độ y của M không thay đổi, và tọa độ x của M luôn là .

Vận dụng 2 trang 161 Tin học 12: Hãy hiển thị mặt phẳng y = x + 3 và mặt trụ (y - 1)² + (z-3)² = 4. Phần giao giữa hai mặt này là hình gì?

Lời giải:

Khi hai hình này giao nhau, hình giao sẽ là một đường cong trong không gian. Cụ thể, nếu ta xem xét phần giao giữa mặt phẳng và mặt trụ, điều này sẽ là một đường cong trên mặt phẳng yz với một độ dốc nhất định.