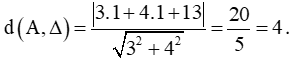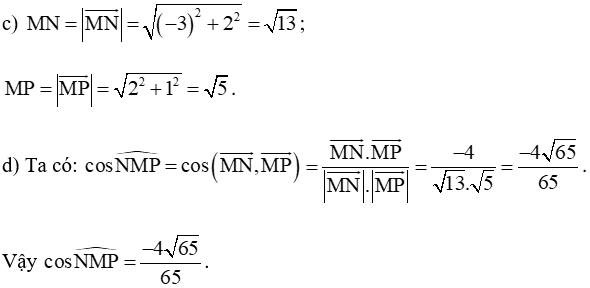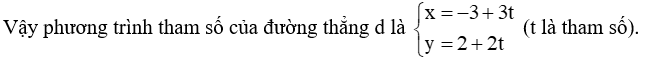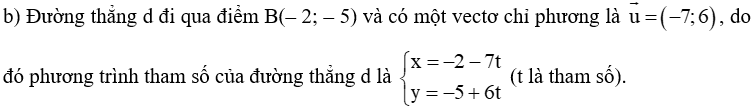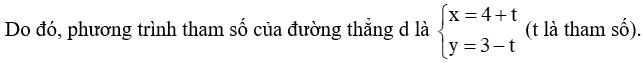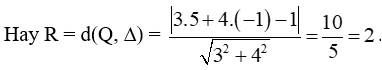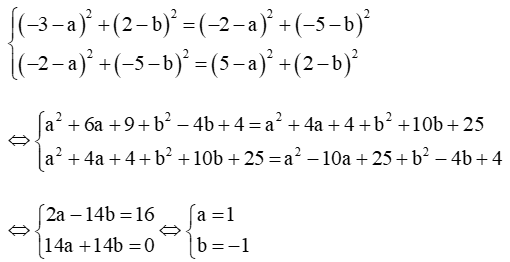Giải Toán 10 trang 103 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 103 Tập 2 trong Bài tập cuối chương 7 Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 103.

Giải Toán 10 trang 103 Tập 2 Cánh diều

Bài 1 trang 103 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(3; 4); B(2; 5). Tọa độ của $\overrightarrow{AB}$ là:

A. (1; –1).

B. (1; 1).

C. (– 1; 1).

D. (– 1; – 1).

Lời giải:

Đáp án đúng là: C.

Ta có: $\overrightarrow{AB}=\left(2-3;5-4\right)$. Vậy $\overrightarrow{AB}=\left(-1;1\right)$.

Bài 2 trang 103 Toán lớp 10 Tập 2: Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng Δ: 2x – 3y + 4 = 0?

A. $\overrightarrow{n_1}=\left(3;2\right)$.

B. $\overrightarrow{n_2}=\left(2;3\right)$.

C. $\overrightarrow{n_3}=\left(3;-2\right)$.

D. $\overrightarrow{n_4}=\left(2;-3\right)$.

Lời giải:

Đáp án đúng là: D.

Đường thẳng ∆: 2x – 3y + 4 = 0 có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$.

Bài 3 trang 103 Toán lớp 10 Tập 2: Tọa độ tâm I của đường tròn (C): (x + 6)² + (y – 12)² = 81 là:

A. (6; – 12).

B. (– 6; 12).

C. (– 12; 6).

D.(12; – 6).

Lời giải:

Đáp án đúng là: B.

Ta có: (x + 6)² + (y – 12)² = 81 ⇔ (x – (– 6))² + (y – 12)² = 9².

Do đó đường tròn (C) có tâm I(– 6; 12).

Bài 4 trang 103 Toán lớp 10 Tập 2: Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 3x + 4y + 13 = 0 bằng:

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải:

Đáp án đúng là: D.

Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 3x + 4y + 13 = 0 là

Bài 5 trang 103 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(2; 1), N(– 1; 3), P(4; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow{OM},\overrightarrow{MN},\overrightarrow{MP}$ ;

b) Tính tích vô hướng $\overrightarrow{MN}.\overrightarrow{MP}$ ;

c) Tính độ dài các đoạn thẳng MN, MP;

d) Tính $cos\widehat{NMP}$ ;

e) Tìm tọa độ trung điểm I của NP và trọng tâm G của tam giác MNP.

Lời giải:

a) Tọa độ của vectơ $\overrightarrow{OM}$ chính là tọa độ của điểm M(2; 1), do đó $\overrightarrow{OM}=\left(2;1\right)$.

Ta có: $\overrightarrow{MN}=\left(-1-2;3-1\right)$, do đó $\overrightarrow{MN}=\left(-3;2\right)$.

$\overrightarrow{MP}=\left(4-2;2-1\right)$, do đó $\overrightarrow{MP}=\left(2;1\right)$.

b) Ta có: $\overrightarrow{MN}.\overrightarrow{MP}=\left(-3\right).2+2.1=-6+2=-4$.

e) Tọa độ trung điểm I của NP là $x_I=\frac{\left(-1\right)+4}{2}=\frac{3}{2};y_I=\frac{3+2}{2}=\frac{5}{2}$ hay $I\left(\frac{3}{2};\frac{5}{2}\right)$.

Tọa độ trọng tâm G của tam giác MNP là $x_G=\frac{2+\left(-1\right)+4}{3}=\frac{5}{3};y_G=\frac{1+3+2}{3}=\frac{6}{3}=2$ hay $G\left(\frac{5}{3};2\right)$.

Bài 6 trang 103 Toán lớp 10 Tập 2: Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:

a) d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$;

b) d đi qua điểm B(– 2; – 5) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(-7;6\right)$;

c) d đi qua hai điểm C(4; 3) và D(5; 2).

Lời giải:

a) Đường thẳng d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$, do đó phương trình tổng quát của đường thẳng d là: 2(x – (– 3)) – 3(y – 2) = 0 hay 2x – 3y + 12 = 0.

Đường thẳng d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$, do đó nó có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;2\right)$.

Đường thẳng d có một vectơ chỉ phương là , suy ra nó có một vectơ pháp tuyến là $\overrightarrow{n}=\left(6;7\right)$.

Vậy phương trình tổng quát của đường thẳng d là 6(x + 2) + 7(y + 5) = 0 hay 6x + 7y + 47 = 0.

c) Ta có: $\overrightarrow{CD}=\left(5-4;2-3\right)=\left(1;-1\right)$.

Đường thẳng d đi qua 2 điểm C, D nên có một vectơ chỉ phương là $\overrightarrow{u}=\overrightarrow{CD}=\left(1;-1\right)$.

Đường thẳng d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;\text{}1\right)$.

Vậy phương trình tổng quát của đường thẳng d là 1(x – 4) + 1(y – 3) = 0 hay x + y – 7 = 0.

Bài 7 trang 103 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong mỗi trường hợp sau:

a) (C) có tâm I(– 4; 2) và bán kính R = 3;

b) (C) có tâm P(3; – 2) và đi qua điểm E(1; 4);

c) (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0;

d) (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).

Lời giải:

a) Đường tròn (C) có tâm I(– 4; 2) và bán kính R = 3.

Vậy phương trình đường tròn (C) là (x – (– 4))² + (y – 2)² = 3² hay (x + 4)² + (y – 2)² = 9.

b) Đường tròn (C) có tâm P(3; – 2) và đi qua điểm E(1; 4) nên bán kính của đường tròn chính bằng khoảng cách từ P đến E.

Do đó, R = PE = $\sqrt{{\left(1-3\right)}^2+{\left(4-\left(-2\right)\right)}^2}=\sqrt{4+36}=\sqrt{40}$.

Vậy phương trình đường tròn (C) là ${\left(x-3\right)}^2+{\left(y-\left(-2\right)\right)}^2={\left(\sqrt{40}\right)}^2$ hay (x – 3)² + (y + 2)² = 40.

c) Đường tròn (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0, do đó bán kính của đường tròn chính bằng khoảng cách từ tâm Q đến đường thẳng ∆.

Vậy phương trình đường tròn (C) là (x – 5)² + (y – (– 1))² = 2² hay (x – 5)² + (y + 1)² = 4.

d) Đường tròn (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).

Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IB = ID ⇔ IA² = IB² = ID².

Vì IA² = IB², IB² = ID² nên

Đường tròn tâm I(1; – 1) bán kính R = ID = $\sqrt{{\left(5-a\right)}^2+{\left(2-b\right)}^2}$ $=\sqrt{{\left(5-1\right)}^2+{\left(2+1\right)}^2}=5$

Phương trình đường tròn (C) là ${\left(x-1\right)}^2+{\left(y-\left(-1\right)\right)}^2=5^2$.

Vậy phương trình đường tròn (C) là ${\left(x-1\right)}^2+{\left(y+1\right)}^2=25$.

Lời giải bài tập Toán lớp 10 Bài tập cuối chương 7 Cánh diều hay khác:

• Giải Toán 10 trang 104 Tập 2