Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P)
Câu hỏi:
Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:
a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau;
Trả lời:
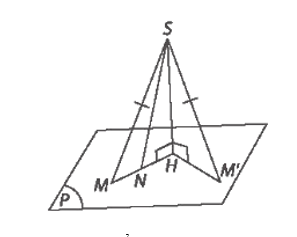
a) Có H là hình chiếu của S trên mặt phẳng (P) nên SH ^ (P), suy ra SH ^ HM, SH ^ HM'.
- Giả sử SM = SM'.
Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2
Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2.
Mà SM = SM' nên HM = HM'.
- Giả sử HM = HM'.
Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2
Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2.
Mà HM = HM' nên SM = SM'.
Vậy hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau.