Toán 11 Bài 16: Giới hạn của hàm số - Kết nối tri thức

Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức

\(m = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\),

trong đó m₀ là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?

Cho hàm số \(f\left( x \right) = \frac{{4 - {x^2}}}{{x - 2}}\).

a) Tìm tập xác định của hàm số f(x).

b) Cho dãy số \({x_n} = \frac{{2n + 1}}{n}\). Rút gọn f(x_n) và tính giới hạn của dãy (u_n) với u_n = f(x_n).

c) Với dãy số (x_n) bất kì sao cho x_n ≠ 2 và x_n ⟶ 2, tính f(x_n) và tìm \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\).

Cho hàm số \(f\left( x \right) = \frac{{\left| {x - 1} \right|}}{{x - 1}}\).

a) Cho \({x_n} = 1 - \frac{1}{{n + 1}}\) và \({x'_n} = 1 + \frac{1}{n}\). Tính y_n = f(x_n) và y'_n = f(x'_n).

b) Tìm giới hạn của các dãy số (y_n) và (y'_n).

c) Cho các dãy số (x_n) và (x'_n) bất kì sao cho x_n < 1 < x'_n và x_n ⟶ 1, x'_n ⟶ 1, tính \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\) và \[\mathop {\lim }\limits_{n \to + \infty } f\left( {{{x'}_n}} \right)\].

Cho hàm số \[f\left( x \right) = \left\{ \begin{array}{l} - x\,\,\,\,\,\,\,n\^e 'u\,\,\,\,x < 0\\\sqrt x \,\,\,\,\,\,n\^e 'u\,\,\,\,x \ge 0.\end{array} \right.\]

Tính \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 0} f\left( x \right)\).

Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.

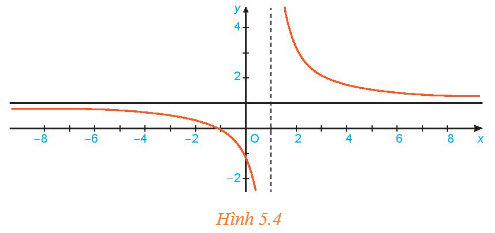
Giả sử (x_n) là dãy số sao cho x_n > 1, x_n ⟶ +∞. Tính f(x_n) và tìm \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\).

Cho tam giác vuông OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h.

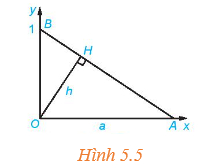
a) Tính h theo a.

b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?

c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?

Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6.

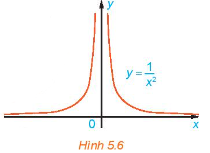
Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng f(x_n) ⟶ +∞.

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 0} \frac{2}{{\left| x \right|}}\);

b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }}\).

Cho hai hàm số \(f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\) và g(x) = x + 1. Khẳng định nào sau đây là đúng?

a) f(x) = g(x);

b) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 0} \frac{{{{\left( {x + 2} \right)}^2} - 4}}{x}\);

b) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 9} - 3}}{{{x^2}}}\).

Cho hàm số \(H\left( t \right) = \left\{ \begin{array}{l}0\,\,\,n\^e 'u\,\,t < 0\\1\,\,\,\,n\^e 'u\,\,t \ge 0\end{array} \right.\) (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thời điểm t = 0).

Tính \(\mathop {\lim }\limits_{t \to {0^ + }} H\left( t \right)\) và \(\mathop {\lim }\limits_{t \to {0^ - }} H\left( t \right)\).

Tính các giới hạn một bên:

a) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{x - 2}}{{x - 1}}\);

b) \(\mathop {\lim }\limits_{x \to {4^ - }} \frac{{{x^2} - x + 1}}{{4 - x}}\).

Cho hàm số \(g\left( x \right) = \frac{{{x^2} - 5x + 6}}{{\left| {x - 2} \right|}}\).

Tìm \(\mathop {\lim }\limits_{x \to {2^ + }} g\left( x \right)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} g\left( x \right)\).

Tính các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 2x}}{{\sqrt {{x^2} + 1} }}\);

b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right)\).

Cho hàm số \(f\left( x \right) = \frac{2}{{\left( {x - 1} \right)\left( {x - 2} \right)}}\).

Tính \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\).