Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b (H.7.21).
Câu hỏi:
Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b (H.7.21).
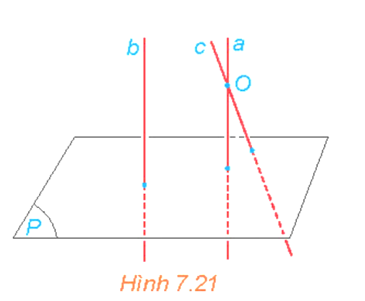
a) Hỏi c có vuông góc với với (P) hay không ? Nêu nhận xét về vị trí tương đối giữa a và c.
b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.
Trả lời:
a) Vì b ^ (P) và c // b nên c ^ (P).
Vì a và c cắt nhau tại O, mà a ^ (P) và c ^ (P) nên a và c trùng nhau.
b) Vì a và c trùng nhau và b // c nên a // b.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).
a) Từ quan sát trên, hãy giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng đi qua B trên sàn nhà.
Xem lời giải »
Câu 2:
b) Giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng trên sàn nhà.
Xem lời giải »
Câu 3:
Nếu đường thẳng ∆ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không?
Xem lời giải »
Câu 4:
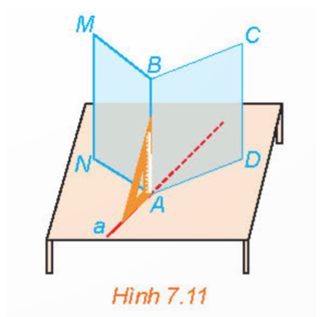
Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bìa thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11.
a) Bằng cách trên, ta tạo đường thẳng AB vuông góc với hai đường thẳng nào thuộc mặt bàn?
Xem lời giải »
Câu 5:
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng ∆ vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (∆, b) và (∆, a). Từ đó rút ra mối quan hệ giữa ∆ và (Q).
Xem lời giải »
Câu 6:
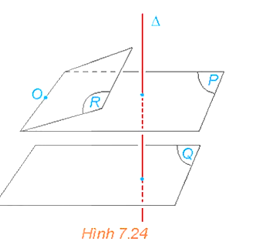
Cho hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng ∆. Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q). (H.7.24).
a) Hỏi (R) có vuông góc với ∆ hay không ? Nêu nhận xét về vị trí tương đối giữa (P) và (R).
Xem lời giải »
Câu 8:
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không ? Vì sao ?
Xem lời giải »