Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A1, A2 sao cho AA1 = A1A2 = A2S. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A1, A2. Mặt phẳng (P) cắt cá
Câu hỏi:
Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A1, A2 sao cho AA1 = A1A2 = A2S. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A1, A2. Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại B1, C1. Mặt phẳng (Q) cắt các cạnh SB, SC lần lượt tại B2, C2. Chứng minh BB1 = B1B2 = B2S và CC1 = C1C2 = C2S.
Trả lời:
Lời giải:
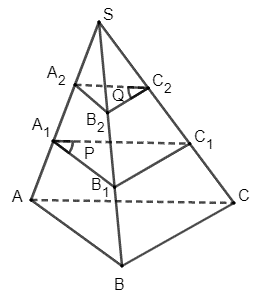
Vì hai mặt phẳng (P) và (Q) song song với mặt phẳng (ABC) nên (P) // (Q), do đó ba mặt phẳng (ABC), (P) và (Q) đôi một song song. Theo định lí Thalés trong không gian, ta suy ra \(\frac{{{A_2}{A_1}}}{{A{A_1}}} = \frac{{{B_2}{B_1}}}{{B{B_1}}} = \frac{{{C_2}{C_1}}}{{C{C_1}}}\).
Mà AA1 = A1A2 nên \[\frac{{{A_2}{A_1}}}{{A{A_1}}} = 1\], suy ra \(\frac{{{A_2}{A_1}}}{{A{A_1}}} = \frac{{{B_2}{B_1}}}{{B{B_1}}} = \frac{{{C_2}{C_1}}}{{C{C_1}}} = 1\), do đó BB1 = B1B2 và CC1 = C1C2.
Sử dụng định lí Thalés ta cũng chứng minh được \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = \frac{{{B_2}S}}{{{B_2}{B_1}}} = \frac{{{C_2}S}}{{{C_2}{C_1}}}\).
Mà A1A2 = A2S nên \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = 1\), suy ra \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = \frac{{{B_2}S}}{{{B_2}{B_1}}} = \frac{{{C_2}S}}{{{C_2}{C_1}}} = 1\), do đó B1B2 = B2S và C1C2 = C2S.
Vậy BB1 = B1B2 = B2S và CC1 = C1C2 = C2S.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Các đầu bếp chuyên nghiệp luôn có kĩ năng dùng dao điêu luyện để thái thức ăn như rau, củ, thịt, cá,... thành các miếng đều nhau và đẹp mắt. Các nhát cắt cần tuân thủ nguyên tắc gì để đạt được điều đó?
Xem lời giải »
Câu 2:
Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.
Xem lời giải »
Câu 3:
Trong hình ảnh mở đầu, các nhát cắt có nằm trong các mặt phẳng song song hay không?
Xem lời giải »
Câu 4:
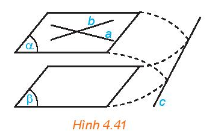
Cho mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) (H.4.41).
Nếu (α) và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?
Xem lời giải »
Câu 5:
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Một mặt phẳng song song với mặt phẳng (A'B'C'D') cắt cạnh bên của hình lăng trụ lần lượt tại A", B", C", D". Hỏi hình tạo bởi các điểm A, B, C, D, A", B", C", D" là hình gì?
Xem lời giải »
Câu 6:
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'.
a) Chứng minh rằng tứ giác AGG'A' là hình bình hành.
b) Chứng minh rằng AGC.A'G'C' là hình lăng trụ.
Xem lời giải »
Câu 7:
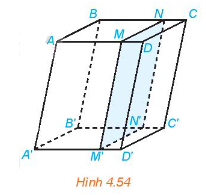
Cho hình hộp ABCD.A'B'C'D'. Một mặt phẳng song song với mặt bên (ABB'A') của hình hộp và cắt các cạnh AD, BC, A'D', B'C' lần lượt tại M, N, M', N' (H.4.54). Chứng minh rằng ABNM.A'B'N'M' là hình hộp.
Xem lời giải »
Câu 8:
Cầu thang xương cá là dạng cầu thang có hình dáng tương tự như những đốt xương cá, thường có những bậc cầu thang với khoảng mở lớn, tạo được sự nhẹ nhàng và thoáng đãng cho không gian sống. Trong Hình 4.55, phần mép của mỗi bậc thang nằm trên tường song song với nhau. Hãy giải thích tại sao.
Xem lời giải »