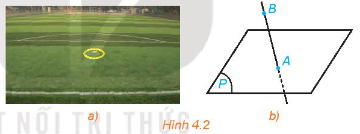
Trong không gian, cho hai đường thẳng a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng? a) Nếu a chứa một điểm nằm trong (P) thì a nằm trong (P). b) Nếu a chứa hai điểm phân biệt th
Câu hỏi:
Trong không gian, cho hai đường thẳng a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng?
a) Nếu a chứa một điểm nằm trong (P) thì a nằm trong (P).
b) Nếu a chứa hai điểm phân biệt thuộc (P) thì a nằm trong (P).
c) Nếu a và b cùng nằm trong (P) thì giao điểm (nếu có) của a và b cũng nằm trong (P).
d) Nếu a nằm trong (P) và a cắt b thì b nằm trong (P).
Trả lời:
Lời giải:
a) Mệnh đề a) là mệnh đề sai vì đường thẳng a có thể cắt mặt phẳng (P).
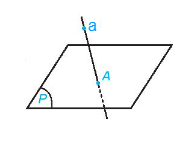
b) Mệnh đề b) là mệnh đề đúng (theo tính chất thừa nhận).
c) Mệnh đề c) là mệnh đề đúng.
Giả sử giao điểm của a và b là H, vì H thuộc a và a nằm trong (P) nên H thuộc (P).
d) Mệnh đề d) là mệnh đề sai.
Chẳng hạn trường hợp như trong hình dưới đây có thể xảy ra: đường thẳng b cắt đường thẳng a tại giao điểm A nhưng đường thẳng b không nằm trong mặt phẳng (P).

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Hãy tìm một số hình ảnh của mặt phẳng trong thực tế.
Xem lời giải »
Câu 2:
Chấm phạt đền trên sân bóng đá cho ta hình ảnh về một điểm thuộc mặt phẳng. Hãy tìm thêm các ví dụ khác cũng gợi cho ta hình ảnh đó.
Xem lời giải »
Câu 3:
Chiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A, B này không?
Xem lời giải »
Câu 4:
Có bao nhiêu đường thẳng đi qua hai điểm trong số ba điểm không thẳng hàng?
Xem lời giải »
Câu 5:
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc cạnh SA, SB và D, E khác S.
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?
b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Xem lời giải »
Câu 6:
Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b tại hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong mặt phẳng (P).
Xem lời giải »
Câu 7:
Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
Xem lời giải »
Câu 8:
Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A). Trong mặt phẳng (ABCD) vẽ một đường thẳng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.
a) Xác định giao điểm của mp(E, d) với các cạnh SB, SD của hình chóp.
b) Xác định giao tuyến của mp(E, d) với các mặt của hình chóp.
Xem lời giải »