Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA (ABCD). Gọi B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD. Chứng minh rằng: a) Các mặt phẳng (AB'C
Câu hỏi:
Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ^ (ABCD). Gọi B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD. Chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
Trả lời:
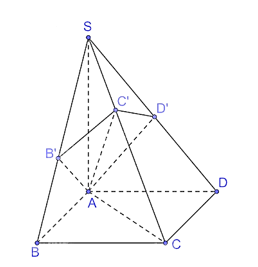
a) Vì B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD nên AB' ^ SB, AC' ^ SC, AD' ^ SD.
Vì SA ^ (ABCD) nên SA ^ BC, SA ^ CD.
Do ABCD là hình chữ nhật nên BC ^ AB, CD ^ AD.
Vì SA ^ BC và BC ^ AB nên BC ^ (SAB), suy ra (SBC) ^ (SAB).
Vì .
Vì SA ^ CD và CD ^ AD nên CD ^ (SAD), suy ra (SCD) ^ (SAD).
Vì .
Vì và nên SC ^ (AB'C'D') mà SC Ì (SAC) nên (SAC) ^ (AB'C'D').
Vì SA ^ (ABCD) mà SA Ì (SAC) nên (SAC) ^ (ABCD).