Giải Toán 12 trang 12 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 12 Tập 2 trong Bài 1: Nguyên hàm Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 12.

Giải Toán 12 trang 12 Tập 2 Chân trời sáng tạo

Bài 5 trang 12 Toán 12 Tập 2: Tìm:

a) $\int x{\left(2x-3\right)}^{2}dx$;                              b) $\int {\sin }^2\frac{x}{2}dx$;

c) $\int {\tan }^{2}xdx$;                                     d) $\int 2^{3x}{.3}^{x}dx$

Lời giải:

a) $\int x{\left(2x-3\right)}^{2}dx=\int x\left(4x^2-12x+9\right)dx$$=\int \left(4x^3-12x^2+9x\right)dx$

$=x^4-4x^3+\frac{9}{2}{x}^2+C$.

b) $\int {\sin }^2\frac{x}{2}dx=\int \frac{1-\cos x}{2}dx$$=\frac{1}{2}\int dx-\frac{1}{2}\int \cos xdx$$=\frac{1}{2}x-\frac{1}{2}\sin x+C$.

c) $\int {\tan }^{2}xdx$$=\int \left(\frac{1}{{\cos }^{2}x}-1\right)dx$$=\int \frac{1}{{\cos }^{2}x}dx-\int dx$$=\tan x-x+C$

d) $\int 2^{3x}{.3}^{x}dx$$=\int 8^x{.3}^{x}dx=\int {24}^{x}dx$$=\frac{{24}^x}{\ln 24}+C$

Bài 6 trang 12 Toán 12 Tập 2: Kí hiệu h(x) là chiều cao của một cây (tính theo mét) sau khi trồng x năm. Biết rằng sau năm đầu tiên cây cao 2 m. Trong 10 năm tiếp theo, cây phát triển với tốc độ $h^{\text{'}}\left(x\right)=\frac{1}{x}$(m/năm).

a) Xác định chiều cao của cây sau x năm (1 ≤ x ≤ 11).

b) Sau bao nhiêu năm cây cao 3 m?

Lời giải:

a) Chiều cao của cây sau x năm là:

$h\left(x\right)=\int h^{\text{'}}\left(x\right)dx=\int \frac{1}{x}dx=\ln x+C$ (1 ≤ x ≤ 11).

Có h(1) = 2 nên  ln1 + C = 2 => C = 2.

Do đó $h\left(x\right)=\ln x+\mathrm{2,}\left(1\le x\le 11\right)$.

b) Cây cao 3 m tức là $\ln x+2=3$$\iff \ln x=1$$\iff x=e\approx \mathrm{2,72}$.

Vậy sau khoảng 2,72 năm thì cây cao 3 m.

Bài 7 trang 12 Toán 12 Tập 2: Một chiếc xe đang chuyển động với vận tốc v₀ = 10 m/s thì tăng tốc với gia tốc không đổi a = 2 m/s². Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc.

Lời giải:

Kí hiệu v(t) là tốc độ của xe, s(t) là quãng đường xe đi được cho đến thời điểm t giây kể từ khi xe tăng tốc.

Vì a(t) = v'(t) với mọi t ≥ 0 nên $v\left(t\right)=\int a\left(t\right)dt=\int 2dt=2t+C$.

Mà v(0) = 10 nên C = 10.

Do đó v(t) = 2t + 10.

Có $s\left(t\right)=\int \left(2t+10\right)dt=t^2+10t+C$.

Vì s(0) = 0 => C = 0.

Do đó s(t) = t² + 10t.

Quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc là:

s(3) = 3² + 10.3 = 39 (m).

Hoạt động khởi động trang 12 Toán 12 Tập 2: Một ô tô đang di chuyển với vận tốc 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t (0 ≤ t ≤ 4). Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

Lời giải:

Sau khi học xong bài này, ta giải quyết bài toán này như sau:

Xe dừng khi v(t) = 20 – 5t = 0 ⇔ t = 4.

Quãng đường xe di chuyển từ khi bắt đầu hãm phanh đến khi dừng là:

$s=\underset{0}{\overset{4}{\int }}v\left(t\right)dt=\underset{0}{\overset{4}{\int }}\left(20-5t\right)dt={\left.\left(20t-\frac{5t^2}{2}\right)\right|}_0^4=40$ (m).

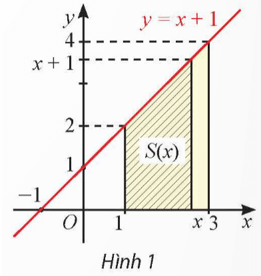
Hoạt động khám phá 1 trang 12 Toán 12 Tập 2: Cho hàm số y = f(x) = x + 1. Với mỗi x ≥ 1, kí hiệu S(x) là diện tích của hình thang giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng vuông góc với Ox tại các điểm có hoành độ 1 và x.

a) Tính S(3).

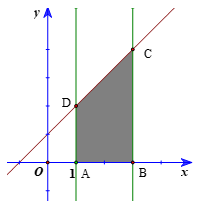
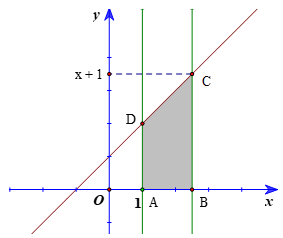
b) Tính S(x) với mỗi x ≥ 1.

c) Tính S'(x). Từ đó suy ra S(x) là một nguyên hàm của f(x) trên [1; +∞).

d) Cho F(x) là một nguyên hàm của hàm số f(x). Chứng tỏ rằng F(3) – F(1) = S(3). Từ đó nhận xét về cách tính S(3) khi biết một nguyên hàm của f(x).

Lời giải:

a)

Gọi A(1; 0), B(3; 0), C, D lần lượt là giao điểm của đường thẳng x = 3; x = 1 với đường thẳng y = x + 1.

Khi đó C(3; 4), D(1; 2).

Ta có S(3) là diện tích của hình thang vuông ABCD với đáy bé AD = 2; đáy lớn BC = 4 và đường cao AB = 2.

Do đó $S\left(3\right)=S_{ABCD}=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(2+4\right).2}{2}=6$.

b)

Tương tự như câu a, ta có A(1; 0), B(x; 0), C(x; x + 1), D(1; 2).

Ta có S(x) là diện tích hình thang ABCD với đáy bé AD = 2, đáy lớn BC = x + 1 và đường cao AB = x – 1.

Do đó $S\left(x\right)=S_{ABCD}=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(x+3\right)\left(x-1\right)}{2}=\frac{x^2+2x-3}{2}$ , x ≥ 1.

c) Có $S^{\text{'}}\left(x\right)={\left(\frac{x^2+2x-3}{2}\right)}^{\text{'}}=\frac{2x+2}{2}=x+1=f\left(x\right)$.

Do đó S(x) là một nguyên hàm của f(x) trên [1; +∞).

d) Vì F(x) là nguyên hàm của hàm số f(x) nên

$F\left(x\right)=\int \left(x+1\right)dx=\frac{x^2}{2}+x+C$.

Do đó $F\left(3\right)=\frac{3^2}{2}+3+C=\frac{15}{2}+C$; $F\left(1\right)=\frac{1^2}{2}+1+C=\frac{3}{2}+C$.

Suy ra $F\left(3\right)-F\left(1\right)=\frac{15}{2}+C-\left(\frac{3}{2}+C\right)=6=S\left(3\right)$.

Để tính S(3), ta cần tìm nguyên hàm F(x) của f(x) và tính S(3) = F(3) – F(1).

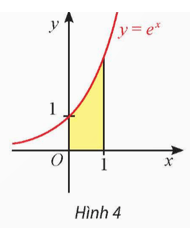
Thực hành 1 trang 13 Toán 12 Tập 2: Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = e^x, trục hoành, trục tung và đường thẳng x = 1 (Hình 4).

Lời giải:

Ta có hàm số y = e^x liên tục, dương trên đoạn [0; 1] .

Ta có $\int e^{x}dx=e^x+C$. Suy ra một nguyên hàm của hàm số y = e^x là F(x) = e^x.

Do đó diện tích hình thang cong cần tính là:

S = F(1) – F(0) = e – 1.

Lời giải bài tập Toán 12 Bài 1: Nguyên hàm hay khác:

• Giải Toán 12 trang 6
• Giải Toán 12 trang 8
• Giải Toán 12 trang 9
• Giải Toán 12 trang 10
• Giải Toán 12 trang 11