Giải Toán 12 trang 67 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 67 Tập 2 trong Bài tập cuối chương 5 Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 67.

Giải Toán 12 trang 67 Tập 2 Chân trời sáng tạo

Bài 10 trang 67 Toán 12 Tập 2: Cho mặt cầu (S): (x + 1)² + (y – 2)² + (z – 1)² = 9. Tọa độ tâm I và bán kính R của (S) là

A. I(−1; 2; 1) và R = 3.

B. I(1; −2; −1) và R = 3.

C. I(−1; 2; 1) và R = 9.

D. I(1; −2; −1) và R = 9.

Lời giải:

Đáp án đúng là: A

Mặt cầu (S): (x + 1)² + (y – 2)² + (z – 1)² = 9 có tâm I(−1; 2; 1) và R = 3.

Bài 11 trang 67 Toán 12 Tập 2: Mặt cầu tâm I(−3; 0; 4) và đi qua điểm A(−3; 0; 0) có phương trình là

A. (x – 3)² + y² + (z + 4)² = 4.

B. (x – 3)² + y² + (z + 4)² = 16.

C. (x + 3)² + y² + (z − 4)² = 16.

D. (x + 3)² + y² + (z − 4)² = 4.

Lời giải:

Đáp án đúng là: C

Bán kính của mặt cầu là $IA=\sqrt{{\left(-3+3\right)}^2+0^2+{\left(0-4\right)}^2}=4$.

Mặt cầu tâm I(−3; 0; 4) và R = 4 có phương trình là (x + 3)² + y² + (z − 4)² = 16.

Bài 12 trang 67 Toán 12 Tập 2: Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(−2; 1; −1).

a) Chứng minh A, B, C, D là bốn đỉnh của một hình chóp.

b) Tìm góc giữa hai đường thẳng AB và CD.

c) Tính độ dài đường cao của hình chóp A.BCD.

Lời giải:

a) Ta có phương trình đoạn chắn của mặt phẳng (ABC) là:

$\frac{x}{1}+\frac{y}{1}+\frac{z}{1}=1$ ⇔ x + y + z – 1 = 0.

Thay tọa độ điểm D vào phương trình mặt phẳng (ABC) ta được:

−2 + 1 −1 −1 = −3 ≠ 0 nên D ∉ (ABC).

Do đó A, B, C, D không đồng phẳng.

Suy ra A, B, C, D là bốn đỉnh của một hình chóp.

b) Đường thẳng AB nhận $\overrightarrow{AB}=\left(-1;1;0\right)$ làm vectơ chỉ phương.

Đường thẳng CD nhận $\overrightarrow{CD}=\left(-2;1;-2\right)$ làm vectơ chỉ phương.

$\cos \left(AB,CD\right)=\frac{\left|\left(-1\right).\left(-2\right)+1.1+0.\left(-2\right)\right|}{\sqrt{{\left(-1\right)}^2+1^2}.\sqrt{{\left(-2\right)}^2+1^2+{\left(-2\right)}^2}}=\frac{3}{3\sqrt{2}}=\frac{1}{\sqrt{2}}$.

Suy ra (AB, CD) = 45°.

c) Có $\overrightarrow{BC}=\left(0;-1;1\right)$, $\overrightarrow{CD}=\left(-2;1;-2\right)$, $\left[\overrightarrow{BC},\overrightarrow{CD}\right]=\left(1;-2;-2\right)$.

Mặt phẳng (BCD) đi qua B(0; 1; 0) và nhận $\overrightarrow{n}=\left[\overrightarrow{BC},\overrightarrow{CD}\right]=\left(1;-2;-2\right)$ làm vectơ pháp tuyến có phương trình là x – 2(y – 1) – 2z = 0 ⇔ x – 2y – 2z + 2 = 0.

Đường cao của hình chóp A.BCD chính là khoảng cách từ A đến mặt phẳng (BCD).

Ta có $d\left(A,\left(BCD\right)\right)=\frac{\left|1+2\right|}{\sqrt{1^2+{\left(-2\right)}^2+{\left(-2\right)}^2}}=1$

Bài 13 trang 67 Toán 12 Tập 2: Cho bốn điểm A(−2; 6; 3), B(1; 0; 6), C(0; 2; −1), D(1; 4; 0).

a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.

b) Tính chiều cao AH của tứ diện ABCD.

c) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.

Lời giải:

a) Ta có $\overrightarrow{BC}=\left(-1;2;-7\right),\overrightarrow{BD}=\left(0;4;-6\right)$, $\left[\overrightarrow{BC},\overrightarrow{BD}\right]=\left(16;-6;-4\right)$

Mặt phẳng (BCD) đi qua B(1; 0; 6) và nhận $\overrightarrow{n}=\frac{1}{2}\left[\overrightarrow{BC},\overrightarrow{BD}\right]=\left(8;-3;-2\right)$ có phương trình là 8(x – 1) – 3y – 2(z – 6) = 0 ⇔ 8x – 3y – 2z + 4 = 0.

Thay tọa độ điểm A vào phương trình mặt phẳng (BCD) ta được:

8.(−2) – 3.6 – 2.3 + 4 = −36 ≠ 0.

Do đó A ∉ (BCD). Suy ra ABCD là một tứ diện.

b) Ta có $AH=d\left(A,\left(BCD\right)\right)=\frac{\left|8.\left(-2\right)-3.6-2.3+4\right|}{\sqrt{8^2+{\left(-3\right)}^2+{\left(-2\right)}^2}}=\frac{36}{\sqrt{77}}$.

c) Ta có $\overrightarrow{AB}=\left(3;-6;3\right)$ và $\overrightarrow{CD}=\left(1;2;1\right)$, $\left[\overrightarrow{AB},\overrightarrow{CD}\right]=\left(-12;0;12\right)$.

Mặt phẳng (α) đi qua A(−2; 6; 3) và nhận $\overrightarrow{n}=-\frac{1}{12}\left[\overrightarrow{AB},\overrightarrow{CD}\right]=\left(1;0;-1\right)$ có phương trình là (x + 2) – (z – 3) = 0 ⇔ x – z + 5 = 0.

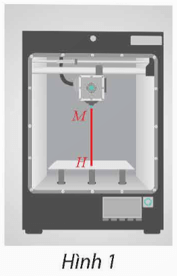
Bài 14 trang 67 Toán 12 Tập 2: Phần mềm điều khiển máy in 3D cho biết đầu in phun của máy đang đặt tại điểm M(3; 4; 24) (đơn vị: cm). Tính khoảng cách từ đầu in đến khay đặt vật in có phương trình z – 4 = 0.

Lời giải:

Gọi (α): z – 4 = 0.

Ta có $d\left(M,\left(\alpha \right)\right)=\frac{\left|24-4\right|}{\sqrt{1^2}}=20$.

Bài 15 trang 67 Toán 12 Tập 2: Cho hai mặt phẳng (P): x – y – 6 = 0 và (Q). Biết rằng điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q). Tính góc giữa mặt phẳng (P) và mặt phẳng (Q).

Lời giải:

Vì điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q) nên mặt phẳng (Q) nhận $\overrightarrow{OH}=\left(2;-1;-2\right)$ làm một vectơ pháp tuyến.

Mặt phẳng (P) có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;-1;0\right)$

$\cos \left(\left(P\right),\left(Q\right)\right)=\frac{\left|2.1+\left(-1\right).\left(-1\right)+\left(-2\right).0\right|}{\sqrt{1^2+{\left(-1\right)}^2}.\sqrt{2^2+{\left(-1\right)}^2+{\left(-2\right)}^2}}=\frac{3}{3\sqrt{2}}=\frac{1}{\sqrt{2}}$

Suy ra ((P), (Q)) = 45°.

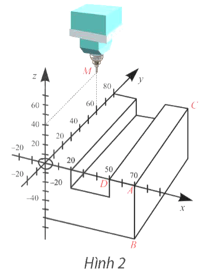
Bài 16 trang 67 Toán 12 Tập 2: Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình 2.

a) Tìm tọa độ các điểm A, B, C, D.

b) Viết phương trình mặt phẳng (ABC) và mặt phẳng (ACD).

c) Viết phương trình tham số của đường thẳng AC.

d) Cho biết đầu mũi tiện đang đặt tại điểm M(0; 60; 40). Tính khoảng cách từ M đến mặt phẳng (ABC).

Lời giải:

a) Ta có A(70; 0; 0), B(70; 0; −60), C(70; 80; 0), D(50; 0; 0).

b) Ta có $\overrightarrow{AB}=\left(0;0;-60\right),\overrightarrow{AC}=\left(0;80;0\right)$, $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(4800;0;0\right)$.

Mặt phẳng (ABC) đi qua A(70; 0; 0), nhận $\overrightarrow{n}=\frac{1}{4800}\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(1;0;0\right)$ có phương trình là x – 70 = 0.

Có $\overrightarrow{AC}=\left(0;80;0\right)$, $\overrightarrow{AD}=\left(-20;0;0\right)$, $\left[\overrightarrow{AC},\overrightarrow{AD}\right]=\left(0;0;1600\right)$

Mặt phẳng (ACD) đi qua A(70; 0; 0), nhận $\overrightarrow{n}=\frac{1}{1600}\left[\overrightarrow{AC},\overrightarrow{AD}\right]=\left(0;0;1\right)$ có phương trình là z = 0.

c) Đường thẳng AC đi qua A(70; 0; 0) và nhận $\overrightarrow{a}=\frac{1}{80}\overrightarrow{AC}=\left(0;1;0\right)$ có phương trình tham số là $\left\{\begin{array}{l}x=70\\ y=t\\ z=0\end{array}\right.$.

d) $d\left(M,\left(ABC\right)\right)=\frac{\left|0-70\right|}{\sqrt{1^2}}=70$.

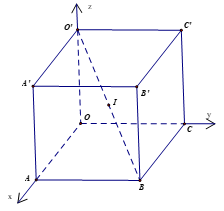
Bài 17 trang 67 Toán 12 Tập 2: Cho hình hộp chữ nhật OABC.O'A'B'C', với O là gốc tọa độ, A(2; 0; 0), C(0; 6; 0), O'(0; 0; 4). Viết phương trình:

a) Mặt phẳng (O'AC);

b) Đường thẳng CO';

c) Mặt cầu đi qua các đỉnh của hình hộp.

Lời giải:

a) Mặt phẳng đoạn chắn của (O'AC) là $\frac{x}{2}+\frac{y}{6}+\frac{z}{4}=1$ ⇔ 6x + 2y + 3z – 12 = 0.

b) Đường thẳng CO' đi qua C(0; 6; 0) nhận $\frac{1}{2}\overrightarrow{C{O}^{\text{'}}}=\left(0;-3;2\right)$ làm vectơ chỉ phương có phương trình là  $\left\{\begin{array}{l}x=0\\ y=6-3t\\ z=2t\end{array}\right.$

c)  Mặt cầu đi qua các đỉnh của hình hộp có tâm I là trung điểm của O'B và bán kính IO'.

Có B(2; 6; 0), O'(0; 0; 4). Suy ra I(1; 3; 2) và $I{O}^{\text{'}}=\sqrt{{\left(-1\right)}^2+{\left(-3\right)}^2+{\left(4-2\right)}^2}=\sqrt{14}$.

Phương trình mặt cầu là: (x – 1)² + (y – 3)² + (z – 2)² = 14.

Bài 18 trang 67 Toán 12 Tập 2: Cho ba điểm A(1; 0; 0), B(0; 2; 0) và C(0; 0; 3). Chứng minh rằng nếu điểm M(x; y; z) thỏa mãn MA² = MB² + MC² thì M thuộc một mặt cầu (S). Tìm tâm và bán kính của (S).

Lời giải:

MA² = MB² + MC²

⇔ (x – 1)² + y² + z² = x² + (y – 2)² + z² + x² + y² + (z – 3)²

⇔ x² – 2x + 1 + y² + z² = x² + y² – 4y + 4 + z² + x² + y² + z² – 6z + 9

⇔ x² + 2x + 1 + y² – 4y + 4 + z² – 6z + 9 – 2 = 0

⇔ (x + 1)² + (y – 2)² + (z – 3)² = 2.

Do đó M luôn thuộc vào mặt cầu S với tâm I(−1; 2; 3) và $R=\sqrt{2}$

Lời giải bài tập Toán 12 Bài tập cuối chương 5 hay khác:

• Giải Toán 12 trang 66