Giải Toán 12 trang 26 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 26 Tập 1 trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 26.

Giải Toán 12 trang 26 Tập 1 Kết nối tri thức

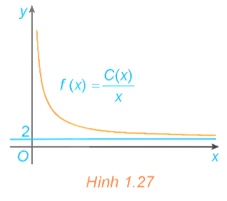
Mở đầu trang 26 Toán 12 Tập 1: Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 45 (triệu đồng). Khi đó chi phí trung bình cho mỗi đơn vị sản phẩm là $f\left(x\right)=\frac{C\left(x\right)}{x}$. Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?

Lời giải:

Có $f\left(x\right)=\frac{C\left(x\right)}{x}=\frac{2x+45}{x}$

Có $f^{\text{'}}\left(x\right)=\frac{-45}{x^2}<\mathrm{0,}\forall x\ge 1$ nên hàm số $f\left(x\right)=\frac{C\left(x\right)}{x}$ là hàm số giảm.

Có $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{2x+45}{x}=\underset{x\to +\infty }{\lim }\frac{2+\frac{45}{x}}{1}=2$

Do đó chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.

Điều này được thể hiện trong Hình 1.27 là đồ thị hàm số $f\left(x\right)=\frac{C\left(x\right)}{x}$ có tiệm cận ngang là đường thẳng y = 2 và đi xuống trong khoảng (0; +∞).

HĐ1 trang 26 Toán 12 Tập 1: Cho hàm số y = x² – 4x + 3. Thực hiện lần lượt các yêu cầu sau:

a) Tính y' và tìm các điểm tại đó y' = 0.

b) Xét dấu y' để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.

c) Tính $\underset{x\to -\infty }{\lim }y,\underset{x\to +\infty }{\lim }y$ và lập bảng biến thiên của hàm số.

d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.

Lời giải:

a) Ta có y' = 2x – 4; y' = 0 ⇔ x = 2.

b) +) y' > 0 ⇔ 2x – 4 > 0 ⇔ x > 2. Hàm số đồng biến trên khoảng (2; +∞).

+) y' < 0 ⇔ 2x – 4 < 0 ⇔ x < 2. Hàm số nghịch biên trên khoảng (−∞; 2).

Ta có x = 2 là điểm cực tiểu của đồ thị hàm số và y_CT = −1.

Hàm số không có cực đại.

c) $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\left(x^2-4x+3\right)=+\infty ,\underset{x\to +\infty }{\lim }\left(x^2-4x+3\right)=+\infty$

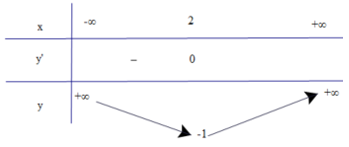
Bảng biến thiên

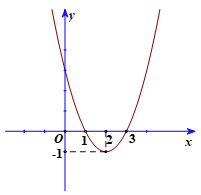
d) Đồ thị hàm số y = x² – 4x + 3

+) Ta có: y = 0 ⇔ x² – 4x + 3 = 0 ⇔ x = 1 hoặc x = 3.

Đồ thị giao với Ox tại (1; 0) và (3; 0).

+) Đồ thị hàm số đi qua điểm (2; −1).

Đồ thị nhận đường thẳng x = 2 là trục đối xứng.

Lời giải bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác:

• Giải Toán 12 trang 29
• Giải Toán 12 trang 32