Bài 3 trang 15 Toán 6 Tập 2 Chân trời sáng tạo | Giải Toán lớp 6
Giải Toán lớp 6 Chân trời sáng tạo Bài 3: So sánh phân số
Bài 3 trang 15 Toán lớp 6 Tập 2: a) So sánh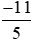
với
với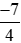 –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
Từ đó suy ra kết quả so sánh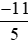
với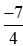
.
b) So sánh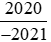 
với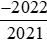
.
Lời giải:
a) Ta có: −2 =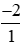
.
Mẫu số thích hợp để so sánh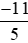
với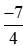
với –2 là mẫu số chung của ba phân số
;
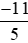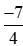và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
Mẫu số chung là 20.
Ta thực hiện:
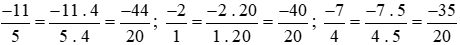
Vì −44 < −40 nên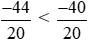
hay
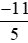< −2.
Vì −40 < −35 nên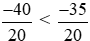 
hay −2 <
.
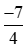Áp dụng tính chất bắc cầu, ta suy ra: < .
Vậy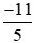 
<
.
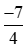b) So sánh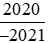
với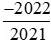
.
Nhận thấy: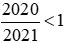
và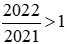
.
Do đó để so sánh hai phân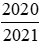
và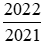
, ta có thể so sánh chúng với 1.
Suy ra ta có thể so sánh hai phân số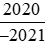 
với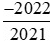
với −1.
Cách 1: So sánh hai phân số trên với −1 và áp dunng tính chất bắc cầu.
Ta có: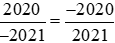
Vì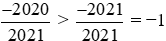 
Và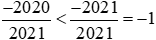
Do đó áp dụng tính chất bắc cầu, ta suy ra: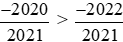
.
Vậy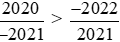 
.
Cách 2: Đưa hai phân số về cùng mẫu dương rồi so sánh:
Ta có: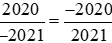
.
Vì −2020 > −2022 nên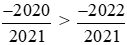
.
Vậy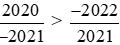
.
Lời giải bài tập Toán 6 Bài 3: So sánh phân số hay, chi tiết khác:
Thực hành 1 trang 13 Toán lớp 6 Tập 2: So sánh (-4)/(-5) và 2/(-5) ....
Thực hành 2 trang 14 Toán lớp 6 Tập 2: So sánh (-7)/18 và 5/(-12) ....
Thực hành 3 trang 14 Toán lớp 6 Tập 2: Viết số nguyên dưới dạng phân số rồi so sánh ....
Thực hành 4 trang 14 Toán lớp 6 Tập 2: So sánh a) (-21)/10 và 0; b) 0 và (-5)/(-2) ....
Bài 1 trang 15 Toán lớp 6 Tập 2: So sánh hai phân số. a) (-3)/8 và (-5)/24; ....
Bài 2 trang 15 Toán lớp 6 Tập 2: Tổ 1 gồm 8 bạn có tổng chiều cao là 115 dm. Tổ 2 gồm 10 bạn ....
Bài 4 trang 15 Toán lớp 6 Tập 2: Sắp xếp các số 2; 5/(-6); 3/5; −1 ....
