Giải Toán lớp 6 Bài 17: Phép chia hết. Ước và bội của một số nguyên - Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán lớp 6 Bài 17: Phép chia hết. Ước và bội của một số nguyên sách Kết nối tri thức với cuộc sống đầy đủ, chính xác nhất giúp các bạn làm bài tập Toán 6 nhanh nhất.
Giải Toán 6 Bài 17: Phép chia hết. Ước và bội của một số nguyên - Kết nối tri thức
Trả lời câu hỏi giữa bài
Luyện tập 1 trang 73 Toán lớp 6 Tập 1:
1. Thực hiện phép chia 135 : 9. Từ đó suy ra thương của các phép chia 135 : (- 9) và
(-135) : (-9)
2. Tính:
a) (-63) : 9;
b) (-24) : (-8).
Lời giải:
1. 135 : 9 = 15
Từ đó ta có: 135 : (-9) = -15; (-135) : (-9) = 15
2. a) (-63) : 9 = - (63 : 9) = -7;
b) (-24) : (-8) = 24 : 8 = 3.
Luyện tập 2 trang 74 Toán lớp 6 Tập 1:
a) Tìm các ước của – 9;
b) Tìm các bội của 4 lớn hơn – 20 và nhỏ hơn 20.
Lời giải:
a) Ta có các ước nguyên dương của 9 là: 1; 3; 9
Do đó tất cả các ước của -9 là: -9; -3; -1; 1; 3; 9
b) Lần lượt nhân 4 với 0; 1; 2; 3; 4; 5; 6… ta được các bội dương của 4 là: 0; 4; 8; 12; 16; 20; 24;…
Do đó các bội của 4 là …; -24; -20; -16; -12; -8; -4; 0; 4; 8; 12; 16; 20; 24;…
Vậy các bội của 4 lớn hơn – 20 và nhỏ hơn 20 là -16; -12; -8; -4; 0; 4; 8; 12; 16.
Tranh luận trang 74 Toán lớp 6 Tập 1:

Không biết Tròn tìm được hai số nguyên nào nhỉ?
Lời giải:
Bạn Tròn tìm được hai số nguyên khác nhau mà và là hai số đối nhau.
Ví dụ 1: Hai số là 3 và - 3
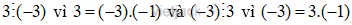
Ví dụ 2: Hai số 12 và - 12
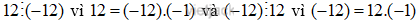
Vậy tổng quát với mọi số nguyên a khác 0. Số đối của a là - a và ta có:
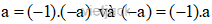
Suy ra a chia hết cho – a và ngược lại (-a) chia hết cho a.
Giải bài tập
Bài 3.39 trang 74 Toán lớp 6 Tập 1:
Tính các thương:
a) 297 : (-3);
b) (-396) : (-12);
c) (-600) : 15.
Lời giải:
a) 297 : (-3) = - (297 : 3) = - 99
b) (-396) : (-12) = 396 : 12 = 33
c) (-600) : 15 = - (600 : 15) = - 40.
Bài 3.40 trang 74 Toán lớp 6 Tập 1:
a) Tìm các ước của mỗi số: 30; 42; - 50.
b) Tìm các ước chung của 30 và 42.
Lời giải:
a) * Tìm các ước của 30:
Ta có: 30 = 2.3.5
Các ước nguyên dương của 30 là: 1; 2; 3; 5; 6; 10; 15; 30
Do đó tất cả các ước của 30 là: -30; -15; -10; -6; -5; -3; -2; -1; 1; 2; 3; 5; 6; 10; 15; 30
* Tìm các ước của 42:
Ta có: 42 = 2. 3. 7
Các ước nguyên dương của 42 là: 1; 2; 3; 6; 7; 14; 21; 42
Do đó tất cả các ước của 42 là: -42; -21; -14; -7; -6; -3; -2; -1; 1; 2; 3; 6; 7; 14; 21; 42
* Tìm các ước của – 50:
Ta có 50 = 2.52
Các ước nguyên dương của 50 là: 1; 2; 5; 10; 25; 50
Do đó tất cả các ước của - 50 là: -50; -25; -10; -5; -2; -1; 1; 2; 5; 10; 25; 50
b) Các ước chung nguyên dương của 30 và 42 là: 1; 2; 3; 6
Do đó các ước chung của 30 và 42 là: -6; -3; -2; -1; 1; 2; 3; 6.
Bài 3.41 trang 74 Toán lớp 6 Tập 1:
Viết tập hợp sau bằng cách liệt kê phần tử:
M = {x ∈ Z | x ⁝ 4 và -16 ≤ x < 20 }
Lời giải:
Vì x là số nguyên chia hết cho 4 nên x là bội của 4.
Lần lượt nhân 4 với 0; 1; 2; 3; 4; 5; 6… ta được các bội dương của 4 là: 0; 4; 8; 12; 16; 20; 24;…
Do đó các bội của 4 là: …; -24; -20; -16; -12; -8; -4; 0; 4; 8; 12; 16; 20; 24
Mà các bội của 4 lớn hơn hoặc bằng - 16 và nhỏ hơn 20 là -16; -12; -8; -4; 0; 4; 8; 12; 16
Vậy M = {-16; -12; -8; -4; 0; 4; 8; 12; 16}.
Bài 3.42 trang 74 Toán lớp 6 Tập 1: Tìm hai ước của 15 có tổng bằng – 4.
Lời giải:
Ta có: 15 = 3. 5
Các ước nguyên dương của 15 là: 1; 3; 5; 15
Do đó tất cả các ước của 15 là: -15; -5; -3; -1; 1; 3; 5; 15
Nhận thấy: (- 5) + 1 = - (5 – 1) = - 4; (-1) + (- 3) = - (1 + 3) = - 4
Vậy hai ước có tổng bằng 4 là – 5 và 1 hoặc – 1 và – 3.
Bài 3.43 trang 74 Toán lớp 6 Tập 1:
Giải thích tại sao: Nếu hai số cùng chia hết cho – 3 thì tổng và hiệu của hai số đó cũng chia hết cho – 3. Hãy thử phát biểu một kết luận tổng quát.
Lời giải:
Giả sử a và b là hai số nguyên cùng chia hết cho -3. Khi đó có hai số nguyên p và q sao cho a = (- 3).p và b = (- 3). q.
+) Ta có: a + b = (-3). p + (- 3). q = (-3). (p + q)
Vì (- 3) ⁝ (- 3) nên (-3). (p + q) ⁝ (- 3) hay (a + b) ⁝ (- 3)
+) Ta có: a - b = (-3). p - (- 3). q = (-3). (p - q)
Vì (- 3) ⁝ (- 3) nên (-3). (p - q) ⁝ (- 3) hay (a - b) ⁝ (- 3)
Vậy nếu hai số cùng chia hết cho – 3 thì tổng và hiệu của hai số đó cũng chia hết cho – 3.
Tổng quát: Nếu hai số nguyên cùng chia hết cho một số nguyên c (c 0) thì tổng (hay hiệu) của chúng cũng chia hết cho c.
Ta có thể chứng minh kết luận trên như sau:
Giả sử a ⁝ c và b ⁝ c có nghĩa là a = cp và b = cq (với p, q ).
Suy ra a + b = cp + cq = c. (p + q).
Vì c ⁝ c nên [c. (p + q)] ⁝ c
Vậy (a + b) ⁝ c.
Tham khảo lời giải bài tập Toán lớp 6 Kết nối tri thức với cuộc sống hay, chính xác nhất khác:

