Bài 3.29 trang 58 Toán 7 Tập 1 - Kết nối tri thức

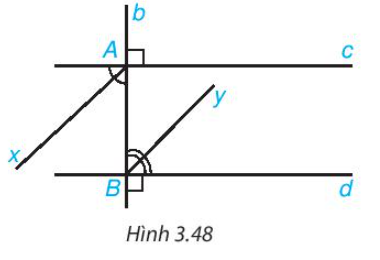
Kẻ các tia phân giác Ax, By của một cặp góc so le trong tạo bởi đường thẳng b vuông góc với hai đường thẳng song song c, d (H.3.48). Chứng minh rằng hai tia phân giác đó nằm trên hai đường thẳng song song.

Giải Toán lớp 7 Luyện tập chung trang 58

Bài 3.29 trang 58 Toán 7 Tập 1: Kẻ các tia phân giác Ax, By của một cặp góc so le trong tạo bởi đường thẳng b vuông góc với hai đường thẳng song song c, d (H.3.48). Chứng minh rằng hai tia phân giác đó nằm trên hai đường thẳng song song.

Lời giải:

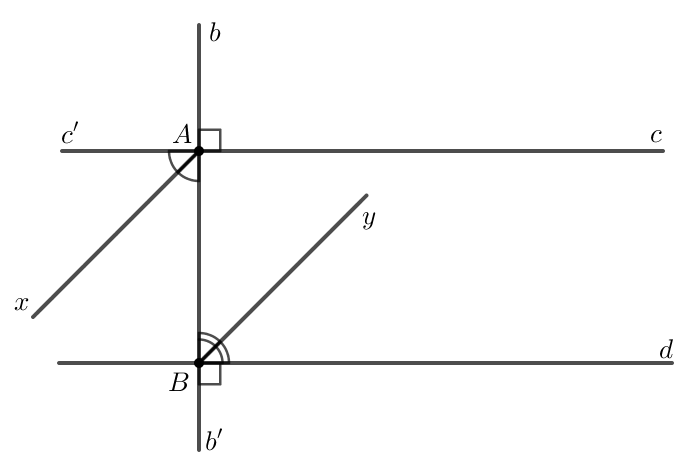
Gọi Ac' là tia đối của tia Ac, Bb' là tia đối của tia BA

Ta có: $\widehat{BA{c}^{\text{'}}}=\widehat{cAb}=90°$ (2 góc đối đỉnh).

Do Ax là tia phân giác của $\widehat{BA{c}^{\text{'}}}$ nên $\widehat{BAx}=\frac{1}{2}\widehat{BA{c}^{\text{'}}}=\frac{1}{2}.90°=45°.$

Ta có $\widehat{dBA}+\widehat{dB{b}^{\text{'}}}=180°$ (2 góc kề bù).

Nên $\widehat{dBA}=180°-\widehat{dB{b}^{\text{'}}}=180°-90°=90°.$

Do By là tia phân giác của $\widehat{dBA}$ nên $\widehat{ABy}=\frac{1}{2}\widehat{dBA}=\frac{1}{2}.90°=45°.$

Khi đó $\widehat{BAx}=\widehat{ABy}=45°.$

Mà hai góc này ở vị trí so le trong nên Ax // By.

Vậy ta có điều phải chứng minh.

Lời giải bài tập Toán lớp 7 Luyện tập chung trang 58 Kết nối tri thức hay khác:

• Bài 3.27 trang 58 Toán 7 Tập 1: Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó. ....

• Bài 3.28 trang 58 Toán 7 Tập 1: Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. ....

• Bài 3.30 trang 58 Toán 7 Tập 1: Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng: ....

• Bài 3.31 trang 58 Toán 7 Tập 1: Cho Hình 3.49. ....