Bài 4.13 trang 73 Toán 7 Tập 1 - Kết nối tri thức

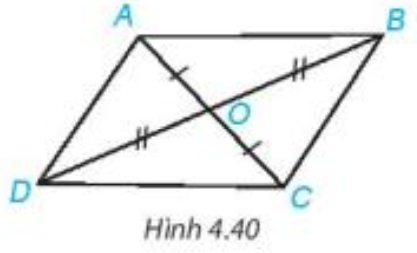
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 4.13 trang 73 Toán 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $\Delta DAB=\Delta BC\text{D}.$

Lời giải:

a) Xét hai tam giác AOD và COB có:

OA = OC (theo giả thiết).

$\widehat{AO\text{D}}=\widehat{COB}$ (2 góc đối đỉnh).

OD = OB (theo giả thiết).

Vậy $\Delta AO\text{D}=\Delta COB$ (c – g – c).

Xét hai tam giác AOB và COD có:

OA = OC (theo giả thiết).

$\widehat{AOB}=\widehat{CO\text{D}}$ (2 góc đối đỉnh).

OB = OD (theo giả thiết).

Vậy $\Delta AOB=\Delta CO\text{D}$ (c – g – c).

b) Do $\Delta AO\text{D}=\Delta COB$ nên AD = BC (2 cạnh tương ứng).

Do $\Delta AOB=\Delta CO\text{D}$ nên AB = CD (2 cạnh tương ứng).

Xét hai tam giác DAB và BCD có:

AD = BC (chứng minh trên).

AB = CD (chứng minh trên).

BD chung.

Vậy $\Delta DAB=\Delta BC\text{D}$ (c – c – c).

Lời giải bài tập Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Kết nối tri thức hay khác:

• Mở đầu trang 70 Toán 7 Tập 1: Trong thực tế, nhiều khi ta không thể đo được hết các cạnh của hai tam giác để khẳng định được chúng có bằng nhau hay không. Khi đó, có cách nào khác giúp ta biết được điều đó? ....

• HĐ1 trang 70 Toán 7 Tập 1: Vẽ $\widehat{xAy}=60°.$ Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm. ....

• HĐ2 trang 70 Toán 7 Tập 1: Vẽ thêm tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ với $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}=60°,A^{\text{'}}{B}^{\text{'}}=4cm$ và $A^{\text{'}}{C}^{\text{'}}=3cm$ (H.4.28). ....

• Câu hỏi trang 71 Toán 7 Tập 1: Trong Hình 4.29, hai tam giác nào bằng nhau? ....

• Luyện tập 1 trang 71 Toán 7 Tập 1: Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao? ....

• Vận dụng trang 71 Toán 7 Tập 1: Cho Hình 4.32, biết $\widehat{OAB}=\widehat{O\text{D}C},$ OA = OD và AB = CD. Chứng minh rằng: ....

• HĐ3 trang 72 Toán 7 Tập 1: Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho $\widehat{xBC}=80°,\widehat{yCB}=40°$ như Hình 4.33. ....

• HĐ4 trang 72 Toán 7 Tập 1: Vẽ thêm tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ sao cho $B^{\text{'}}{C}^{\text{'}}=3cm,\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=80°,\widehat{A^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}}=40°$ (H.4.34). ....

• Câu hỏi trang 72 Toán 7 Tập 1: Hai tam giác nào trong Hình 4.35 bằng nhau? ....

• Luyện tập 2 trang 73 Toán 7 Tập 1: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau. ....

• Thử thách nhỏ trang 73 Toán 7 Tập 1: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao? ....

• Bài 4.12 trang 73 Toán 7 Tập 1: Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau. ....

• Bài 4.14 trang 73 Toán 7 Tập 1: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau. ....

• Bài 4.15 trang 73 Toán 7 Tập 1: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng: ....