Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng

Câu hỏi:

Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8).

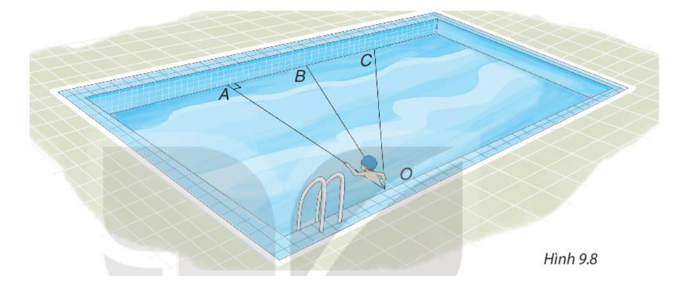
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?

Trả lời:

Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.

Bài toán đưa về tìm đoạn ngắn nhất trong ba đoạn thẳng OA, OB và OC.

$Δ O A B$ có $\hat{O A B}$ = 90^o nên $\hat{O A B}$ là góc lớn nhất trong $Δ O A B$ .

Do đó OB > OA (1).

$\hat{O B C}$ là góc ngoài tại đỉnh B của $Δ O A B$ nên $\hat{O B C} = \hat{B O A} + \hat{O A B} > \hat{O A B}$ .

Do đó $\hat{O B C}$ là góc tù.

Xét $Δ B O C$ có $\hat{O B C}$ là góc tù nên $Δ O B C$ là tam giác tù.

Do đó cạnh OC đối diện với $\hat{O B C}$ là cạnh lớn nhất trong $Δ B O C$ .

Khi đó OC > OB (2).

Từ (1) và (2) suy ra OC > OB > OA.

Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.

Câu 1:

Cho điểm A không nằm trên đường thẳng d.

a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.

Câu 2:

b) Em hãy giải thích vì sao AH < AM.

Câu 3:

Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

Câu 4:

b) So sánh hai đoạn thẳng AB và AM.

Giải Toán lớp 7 Kết nối tri thức