Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.
Câu hỏi:
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.
Trả lời:
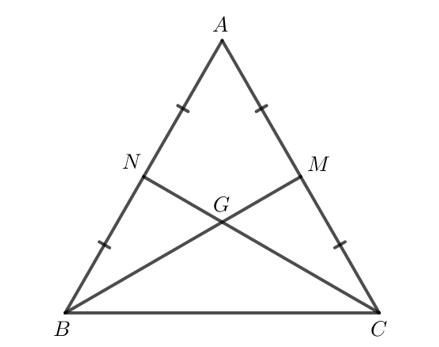
Giả sử tam giác đều ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm G.
Do DABC đều nên DABC cân tại A.
Theo kết quả của câu a, Ví dụ 1, trang 78, 79 ta có:
AM là đường trung tuyến của tam giác ABC nên AM là đường trung trực của cạnh BC.
Tương tự, ta cũng có:
• DABC đều nên DABC cân tại B, do đó BN là đường trung trực của cạnh AC;
• DABC đều nên DABC cân tại C, do đó CP là đường trung trực của cạnh AB.
Mà ba đường trung trực AM, BN và CP cắt nhau tại trọng tâm G
Do đó G cách đều ba đỉnh của tam giác ABC.
Vậy trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.