Giải Toán 7 trang 101 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 101 Tập 2 trong Luyện tập 2 Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 101.

Giải Toán 7 trang 101 Tập 2 Kết nối tri thức

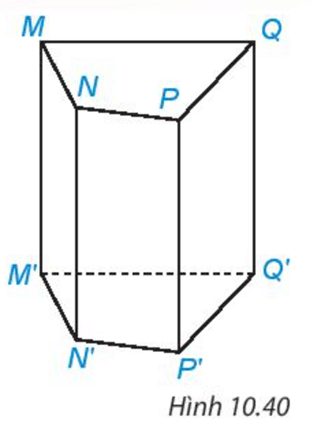
Bài 10.17 trang 101 Toán 7 Tập 2: Viết tên đỉnh, cạnh, mặt bên, mặt đáy của hình lăng trụ đứng tứ giác ở Hình 10.40.

Lời giải:

Các đỉnh của hình lăng trụ tứ giác trên: M, N, P, Q, M’, N’, P’, Q’.

Các cạnh của hình lăng trụ tứ giác trên là: MN, NP, PQ, QM, M’N’, N’P’, P’Q’, Q’M’, MM’, NN’, PP’, QQ’.

Các mặt bên của hình lăng trụ tứ giác trên là: MNN’M’, NPP’N’, PQQ’P’, MQQ’M’.

Các mặt đáy của hình lăng trụ tứ giác trên là: MNPQ, M’N’P’Q’.

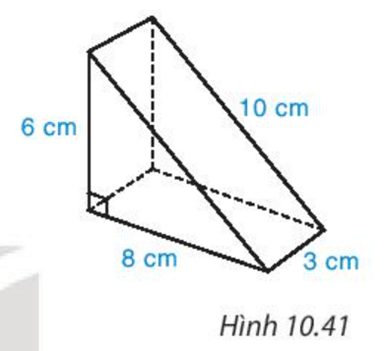
Bài 10.18 trang 101 Toán 7 Tập 2: Một cái bánh ngọt có dạng hình lăng trụ đứng tam giác, kích thước như Hình 10.41.

a) Tính thể tích cái bánh.

b) Nếu phải làm một chiếc hộp để cái bánh này thì diện tích vật liệu cần dùng là bao nhiêu (coi mép dán không đáng kể)?

Lời giải:

a) Diện tích đáy của chiếc bánh là: <![if !vml]><![endif]>. 6 . 8 = 24 (cm²).

Thể tích của chiếc bánh là: 24 . 3 = 72 (cm³).

b) Diện tích xung quanh của chiếc bánh là: (6 + 8 + 10) . 3 = 72 (cm²).

Diện tích hai đáy của chiếc bánh là: 2 . 24 = 48 (cm²).

Diện tích vật liệu cần dùng để làm chiếc hộp là: 72 + 48 = 120 (cm²).

Vậy diện tích vật liệu cần dùng để làm chiếc hộp là 120 cm².

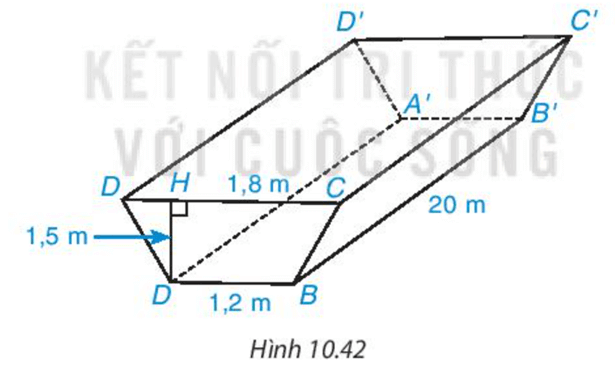
Bài 10.19 trang 101 Toán 7 Tập 2: Người ta đào một đoạn mương có dạng hình lăng trụ đứng tứ giác như Hình 10.42. Biết mương có chiều dài 20 m, sâu 1,5 m, trên bề mặt có chiều rộng 1,8 m và đáy mương là 1,2 m. Tính thể tích đất phải đào lên.

Lời giải:

Coi đoạn mương là một hình lăng trụ đứng ABCD.A’B’C’D’ thì hai mặt đáy của hình lăng trụ đứng là ABCD và A’B’C’D’.

Diện tích mặt đáy của hình lăng trụ là: $\frac{1}{2}$. (1,8 + 1,2) . 1,5 = 2,25 (m²).

Thể tích đất phải đào lên là: 2,25 . 20 = 45 (m³).

Vậy thể tích đất phải đào lên là 45 m³.