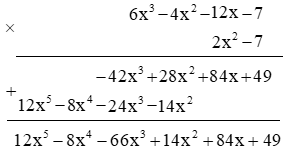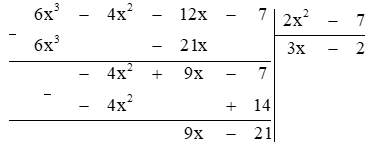Giải Toán 7 trang 110 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 110 Tập 2 trong Bài tập ôn tập cuối năm Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 110.

Giải Toán 7 trang 110 Tập 2 Kết nối tri thức

Bài 1 trang 110 Toán 7 Tập 2: Tính giá trị của các biểu thức sau:

a) $\sqrt{25}$ + (2² . 3)² . ${\left(-\frac{1}{4}\right)}^2$+ 2020⁰ + $\left|-\frac{1}{4}\right|$;

b) $\frac{3^2-0,25.\left(7,5-5,1\right)}{-6,2+2.\left(0,5+1,6\right)}$.

Lời giải:

a) $\sqrt{25}$ + (2² . 3)² . ${\left(-\frac{1}{4}\right)}^2$+ 2020⁰ + $\left|-\frac{1}{4}\right|$;

= 5 + ${\left(\mathrm{4.3.}\frac{-1}{4}\right)}^2$ + 1 + $\frac{1}{4}$

= 5 + (-3)² + 1 + $\frac{1}{4}$

= 5 + 9 + 1 + $\frac{1}{4}$

= 15 + $\frac{1}{4}$

= $\frac{60}{4}+\frac{1}{4}$

= $\frac{61}{4}$.

b) $\frac{3^2-0,25.\left(7,5-5,1\right)}{-6,2+2.\left(0,5+1,6\right)}$.

= $\frac{9-0,25.2,4}{-6,2+2.2,1}$

= $\frac{9-0,6}{-6,2+4,2}$

= $\frac{8,4}{-2}$

= -4,2.

Bài 2 trang 110 Toán 7 Tập 2: Tính một cách hợp lí.

a) $\frac{5}{11}-\frac{10}{19}+1,5+\frac{17}{11}-\frac{9}{19}$;

b) $2\frac{3}{5}.\left(-\frac{2}{3}\right)-2\frac{1}{3}.\left(-\frac{2}{3}\right)+{\left(\frac{2}{3}\right)}^2$

Lời giải:

a) $\frac{5}{11}-\frac{10}{19}+1,5+\frac{17}{11}-\frac{9}{19}$;

= $\frac{5}{11}+\frac{17}{11}+1,5-\frac{9}{19}-\frac{10}{19}$

= $\left(\frac{5}{11}+\frac{17}{11}\right)+1,5-\left(\frac{9}{19}+\frac{10}{19}\right)$

= $\frac{22}{11}+1,5-\frac{19}{19}$

= 2 + 1,5 - 1

= 2,5

b) $2\frac{3}{5}.\left(-\frac{2}{3}\right)-2\frac{1}{3}.\left(-\frac{2}{3}\right)+{\left(\frac{2}{3}\right)}^2$

= $2\frac{3}{5}.\left(-\frac{2}{3}\right)-2\frac{1}{3}.\left(-\frac{2}{3}\right)+{\left(-\frac{2}{3}\right)}^2$

= $\frac{-2}{3}.\left(2\frac{3}{5}-2\frac{1}{3}-\frac{2}{3}\right)$

= $\frac{-2}{3}.\left(2+\frac{3}{5}-2-\frac{1}{3}-\frac{2}{3}\right)$

= $\frac{-2}{3}.\left(2-2+\frac{3}{5}-\frac{1}{3}-\frac{2}{3}\right)$

= $\frac{-2}{3}.\left(\frac{3}{5}-1\right)$

= $\frac{-2}{3}.\frac{-2}{5}$

= $\frac{4}{15}$.

Bài 3 trang 110 Toán 7 Tập 2:

a) Tìm x, biết $\frac{2}{5}$x + $\frac{3}{2}$ = $\frac{3}{5}-\left(-\frac{1}{4}\right)$ .

b) Có hay không số x thỏa mãn điều kiện: $\left(x\right)+\frac{1}{5}=-\left(\frac{1}{2}-\frac{1}{3}\right)$ ?

c) Hãy ước tính (không tra bảng hay dùng máy tính) số dương x (lấy đến 1 chữ số sau dấu phẩy) sao cho x² = 13. Sau đó dùng máy tính cầm tay (hoặc tra bảng) để tính x, chính xác đến hàng phần chục để kiểm tra xem con số em ước tính chênh lệch bao nhiêu so với kết quả tính bằng máy tính.

Lời giải:

a) $\frac{2}{5}$x + $\frac{3}{2}$ = $\frac{3}{5}-\left(-\frac{1}{4}\right)$

$\frac{2}{5}$x + $\frac{3}{2}$ = $\frac{3}{5}+\frac{1}{4}$

$\frac{2}{5}$x = $\frac{3}{5}+\frac{1}{4}-\frac{3}{2}$

$\frac{2}{5}$x = $\frac{12}{20}+\frac{5}{20}-\frac{30}{20}$

$\frac{2}{5}$x = $\frac{-13}{20}$

x = $\frac{-13}{20}:\frac{2}{5}$

x = $\frac{-13}{20}.\frac{5}{2}$

x = $\frac{-13}{8}$

Vậy x = $\frac{-13}{8}$ .

b) $-\left(\frac{1}{2}-\frac{1}{3}\right)=-\left(\frac{3}{6}-\frac{2}{6}\right)=\frac{-1}{6}$ < 0.

Ta có ≥ 0 với mọi giá trị của x nên $\left(x\right)$ + $\frac{1}{5}$ > 0 với mọi giá trị của x.

Do đó không tồn tại giá trị của x để $\left(x\right)$ + $\frac{1}{5}$ = $-\left(\frac{1}{2}-\frac{1}{3}\right)$ .

c) Ta thấy 3² = 9 < 13 < 16 = 4² và 13 – $\frac{1}{2}$ (9 + 16) < 1 nên dự đoán x ≈ $\frac{1}{2}$(3 + 4) = 3,5.

Sử dụng máy tính cầm tay, lấy chính xác đến hàng phần chục ta được $\sqrt{13}$ ≈ 3,6.

Con số ước tính chênh lệch 3,6 – 3,5 = 0,1 so với kết quả tính bằng máy tính.

Bài 4 trang 110 Toán 7 Tập 2: Hai người thợ cùng làm tổng cộng được 136 sản phẩm (thời gian làm như nhau). Hỏi mỗi người thợ làm được bao nhiêu sản phẩm, biết rằng người thợ thứ nhất làm một sản phẩm mất 9 phút, còn người thứ hai làm mất 8 phút?

Lời giải:

Gọi số sản phẩm làm được của người thứ nhất và người thứ hai lần lượt là x và y sản phẩm (x, y ∈ ℕ*).

Tỉ lệ thời gian làm được 1 sản phẩm của người thứ nhất và người thứ hai là $\frac{9}{8}$ .

Thời gian làm và số sản phẩm làm được của hai người là hai đại lượng tỉ lệ nghịch.

Do đó tỉ lệ số sản phẩm làm được của người thứ nhất và người thứ hai là $\frac{8}{9}$ .

Khi đó $\frac{x}{y}=\frac{8}{9}$ nên $\frac{x}{8}=\frac{y}{9}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có: $\frac{x}{8}=\frac{y}{9}=\frac{x+y}{8+9}=\frac{136}{17}=8$

Khi đó x = 8 . 8 = 64, y = 8 . 9 = 72.

Vậy số sản phẩm làm được của người thứ nhất và người thứ hai lần lượt là 64 sản phẩm và 72 sản phẩm.

Bài 5 trang 110 Toán 7 Tập 2: Ba khối 6, 7, 8 của một trường Trung học cơ sở tham gia quyên góp vở tặng các bạn vùng khó khăn. Biết rằng số vở quyên góp được của ba khối theo thứ tự tỉ lệ thuận với 8, 7, 6 và số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là 80 quyển. Hỏi mỗi khối quyên góp được bao nhiêu quyển vở?

Lời giải:

Gọi số vở quyên góp được của ba khối 6, 7, 8 lần lượt là x, y, z quyển (x, y, z ∈ ℕ*).

Do số vở quyên góp được của ba khối tỉ lệ thuận với 8, 7, 6 nên $\frac{x}{8}=\frac{y}{7}=\frac{z}{6}$ .

Do số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là 80 quyển nên

x – z = 80.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{8}=\frac{y}{7}=\frac{z}{6}=\frac{x-z}{8-6}=\frac{80}{2}=40$

Khi đó x = 8 . 40 = 320, y = 7 . 40 = 280, z = 6 . 40 = 240.

Vậy số vở quyên góp được của ba khối 6, 7, 8 lần lượt là 320 quyển, 280 quyển, 240 quyển.

Bài 6 trang 110 Toán 7 Tập 2: Cho hai đa thức A = 6x³ – 4x² – 12x – 7 và B = 2x² – 7.

a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho.

b) Tính giá trị của đa thức A + B tại x = –2.

c) Chứng minh rằng x = 0, x = –1 và x = 2 là ba nghiệm của đa thức A – B.

d) Thực hiện phép nhân A . B bằng hai cách.

e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu A - R chia hết cho B.

Lời giải:

a) +) Xét đa thức A = 6x³ – 4x² – 12x – 7

Đa thức A có hạng tử có bậc cao nhất là 6x³ nên hệ số cao nhất là 6.

Hạng tử có bậc bằng 0 trong đa thức A là –7 nên hệ số tự do là –7.

+) Xét đa thức B = 2x² – 7

Đa thức B có hạng tử có bậc cao nhất là 2x² nên hệ số cao nhất là 2.

Hạng tử có bậc bằng 0 trong đa thức B là –7 nên hệ số tự do là –7.

b) A + B = 6x³ - 4x² - 12x - 7 + 2x² - 7

A + B = 6x³ + (-4x² + 2x²) - 12x + (-7 - 7)

A + B = 6x³ - 2x² - 12x - 14

Thay x = -2 vào đa thức A + B ta được:

A + B = 6 . (-2)³ - 2 . (-2)² - 12 . (-2) - 14

A + B = 6 . (-8) - 2.4 - (-24) - 14

A + B = -48 - 8 + 24 - 14

A + B = -46

Vậy A + B = -46 tại x = -2.

c) A - B = (6x³ - 4x² - 12x - 7) - (2x² - 7)

A - B = 6x³ - 4x² - 12x - 7 - 2x² + 7

A - B = 6x³ + (-4x² - 2x²) - 12x + (-7 + 7)

A - B = 6x³ - 6x² - 12x

Tại x = 0 thì A - B = 6 . 0³ - 6 . 0² - 12 . 0 = 0.

Tại x = -1 thì A - B = 6 . (-1)³ - 6 . (-1)² - 12 . (-1) = -6 - 6 + 12 = 0.

Tại x = 2 thì A - B = 6.2³ - 6.2² - 12.2 = 6.8 - 6.4 - 24 = 0.

Vậy x = 0, x = -1 và x = 2 là ba nghiệm của đa thức A - B.

d) Cách 1. Bỏ dấu ngoặc

A . B = (6x³ - 4x² - 12x - 7) . (2x² - 7)

A . B = [6x³ + (-4x²) + (-12x) + (-7)] . [2x² + (-7)]

A . B = 6x³ . 2x² + 6x³ . (-7) + (-4x²) . 2x² + (-4x²) . (-7) + (-12x) . 2x² + (-12x) . (-7) + (-7) . 2x² + (-7) . (-7)

A . B = 12x⁵ + (-42 x³) + (-8 x⁴) + 28x² + (-24x³) + 84x + (-14x²) + 49

A . B = 12x⁵ - 8x⁴ + (-42 x³ - 24x³) + (28x² - 14x²) + 84x + 49

A . B = 12x⁵ - 8x⁴ - 66x³ + 14x² + 84x + 49

Cách 2. Đặt phép tính

e) Đặt phép chia A cho B ta được:

Đa thức A chia cho đa thức B dư 9x - 21.

Do đó để A - R chia hết cho B và bậc của đơn thức R nhỏ hơn 2 thì đa thức R bằng

9x - 21.

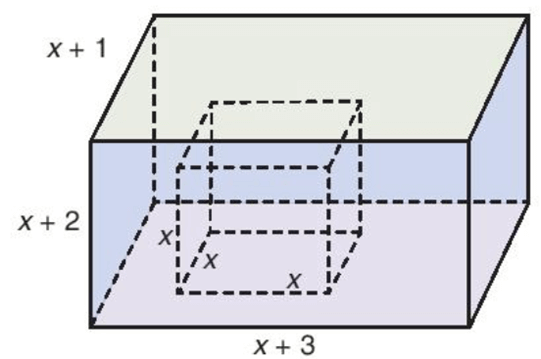
Bài 7 trang 110 Toán 7 Tập 2: Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x (dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng x + 1, x + 3 và x + 2 (xem hình bên).

a) Tìm đa thức biểu thị thể tích nước còn lại trong bể.

b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a.

c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị: dm³) khi x = 7 dm.

Lời giải:

Do bể đầy nước nên khi thả khối lập phương vào thì lượng nước trào ra ngoài bằng thể tích của khối lập phương.

a) Thể tích của bể là: (x + 1)(x + 3)(x + 2) dm³.

Thể tích khối gỗ là: x³ dm³.

Thể tích nước còn lại trong bể là: (x + 1)(x + 3)(x + 2) - x³

= (x.x + x.3 + 1.x + 1.3)(x + 2) - x³

= (x² + 4x + 3)(x + 2) - x³

= (x².x + x².2 + 4x.x + 4x.2 + 3.x + 3.2) - x³

= x³ + 2x² + 4x² + 8x + 3x + 6 - x³

= (x³ - x³) + (2x² + 4x²) + (8x + 3x) + 6

= 6x² + 11x + 6

Vậy thể tích nước còn lại trong bể bằng 6x² + 11x + 6 dm³.

b) Đa thức 6x² + 11x + 6 có hạng tử có bậc cao nhất là 6x² nên bậc của đa thức đó bằng 2, hệ số cao nhất bằng 6.

Hạng tử có bậc bằng 0 trong đa thức đó bằng 6 nên hệ số tự do bằng 6.

c) Tại x = 7 dm, thể tích nước còn lại trong bể bằng:

6 . 7² + 11 . 6 + 6 = 6 . 49 + 66 + 6 = 366 dm³.

Lời giải bài tập Toán lớp 7 Bài tập ôn tập cuối năm Kết nối tri thức hay khác:

• Giải Toán 7 trang 111 Tập 2

• Giải Toán 7 trang 112 Tập 2

• Giải Toán 7 trang 113 Tập 2