Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD
Câu hỏi:
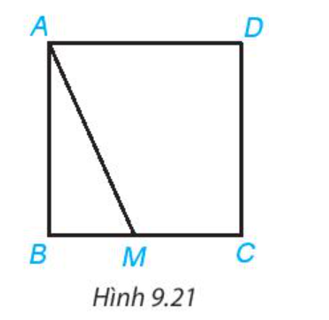
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.21).
Trả lời:
Nếu M trung với B hoặc D thì độ dài AM chính là độ dài hình cạnh hình vuông ABCD.
Với M khác B và thuộc cạnh BC thì AM, AB lần lượt là đường xiên, đường vuông góc kẻ từ A đến BC.
Do đó AM > AB.
Tương tự, khi M khác D và thuộc cạnh CD thì AM > AD.
Mà AB = AD là độ dài cạnh của hình vuông ABCD.
Khi đó AM luôn lớn hơn độ dài cạnh của hình vuông ABCD.
Vậy nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó.

