Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh
Câu hỏi:
Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Trả lời:
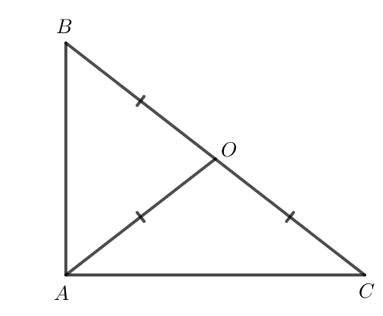
Giả sử O nằm trên cạnh BC của tam giác ABC, khi đó OA = OB = OC (O cách đều ba đỉnh của tam giác).
Vì OA = OB nên tam giác OAB cân tại O
Suy ra,
Vì OA = OC nên tam giác OAC cân tại O
Suy ra,
Xét tam giác ABC ta có:
Lại có: Khi đó hay .
Suy ra
Nên .
Do đó, tam giác ABC vuông tại A.
Vậy nếu O nằm trên một cạnh của tam giác ABC và O cách đều ba đỉnh của tam giác ABC thì ABC là một tam giác vuông.
Xem thêm lời giải bài tập Toán 7 Kết nối tri thức hay, chi tiết:
Câu 1:
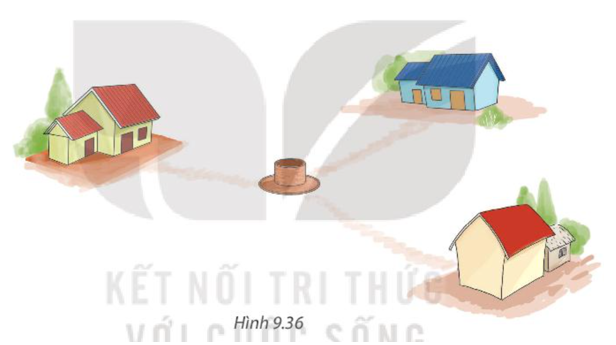
Có thể coi ba ngôi nhà của ba anh em trong một khu vườn là ba đỉnh của một tam giác (không tù). Họ muốn khoan một giếng chung trong vườn cách đều ba ngôi nhà (H.9.36). Em có thể giúp họ chọn địa điểm để khoan giếng không?
Xem lời giải »
Câu 3:
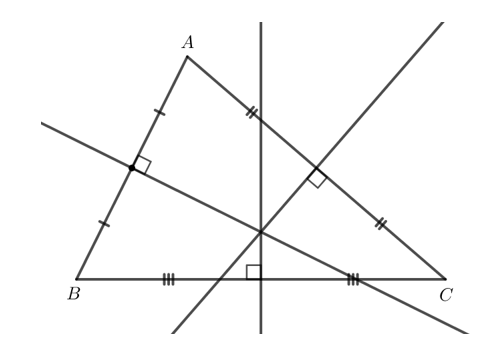
Vẽ tam giác ABC (không tù) và ba đường trung trực của các đoạn thẳng BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm không.
Xem lời giải »
Câu 4:
Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38).
a) Tại sao OB = OC, OC = OA?
Xem lời giải »
Câu 5:
a) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy (H.9.46). Làm thế nào để xác định được bán kính của đường viền này?
Xem lời giải »
Câu 6:
b) Trên bản đồ, ba khu dân cư được quy hoạch tại ba điểm A, B, C không thẳng hàng. Hãy tìm trên bản đồ đó một điểm M cách đều A, B, C để quy hoạch một trường học.
Xem lời giải »
Câu 7:
Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47).
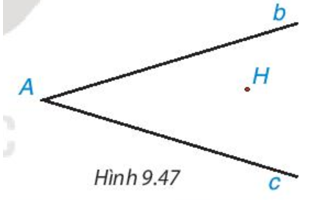
Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Xem lời giải »