Bài 4 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 4 trang 78 Toán 8 Tập 1: Cho hai hàm số $y = - \frac{1}{2} x + 3; y = 2 x - 2.$

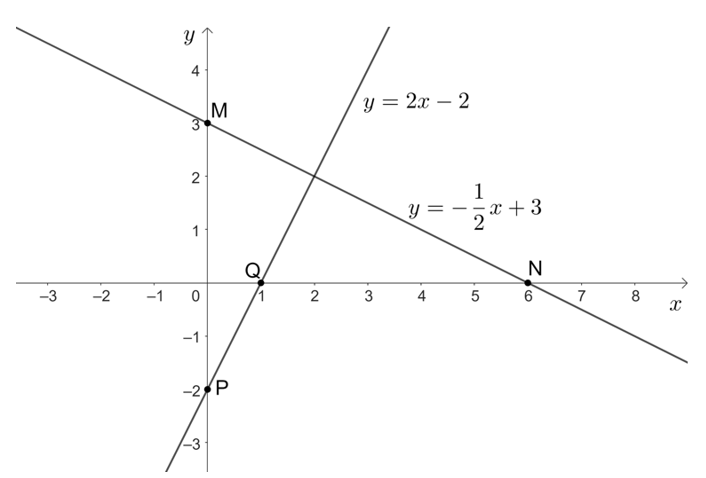
a) Vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ.

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y = - \frac{1}{2} x + 3; y = 2 x - 2.$ với trục hoành và C là giao điểm của hai đường thẳng đó. Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là centimét).

Lời giải:

Cho hai hàm số $y = - \frac{1}{2} x + 3; y = 2 x - 2.$

a) * Hàm số $y = - \frac{1}{2} x + 3$ .

• Với x = 0 thì $y = - \frac{1}{2} . 0 + 3 = 0 + 3 = 3$ , ta được điểm M(0; 3) thuộc đồ thị của hàm số $y = - \frac{1}{2} x + 3$

• Với y = 0 thì $- \frac{1}{2} x + 3 = 0$ suy ra x = 6, ta được điểm N(6; 0) thuộc đồ thị của hàm số $y = - \frac{1}{2} x + 3.$

Do đó, đồ thị của hàm số $y = - \frac{1}{2} x + 3.$ là đường thẳng đi qua hai điểm M(0; 3) và N(6; 0).

* Hàm số y = 2x – 2.

• Với x = 0 thì y = 2 . 0 – 2 = 0 – 2 = – 2 , ta được điểm P(0; – 2) thuộc đồ thị của hàm số y = 2x – 2.

• Với y = 0 thì 2x – 2 = 0 suy ra x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = 2x – 2.

Do đó, đồ thị của hàm số y = 2x – 2 là đường thẳng đi qua hai điểm P(0; – 2) và Q(1; 0).

Ta vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ như sau:

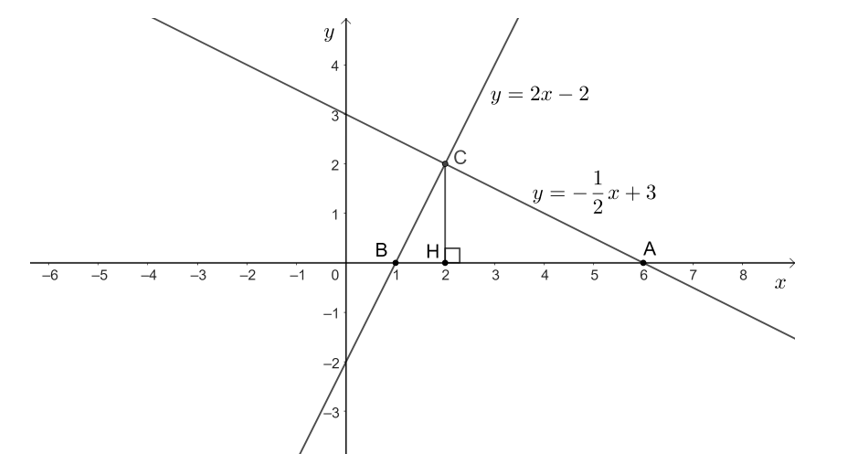
Bài 4 trang 78 Toán 8 Tập 1 Cánh diều | Giải Toán 8

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y = - \frac{1}{2} x + 3; y = 2 x - 2$ với trục hoành và C là giao điểm của hai đường thẳng đó.

Khi đó A ≡ N; B ≡ Q.

Gọi H là hình chiếu của C trên AB hay CH là đường cao của tam giác ABC.

Ta có đồ thị hàm số như sau:

Bài 4 trang 78 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Dựa vào hình vẽ, ta có:

• Tọa độ điểm C là C(2; 2);

• H là hình chiếu của C trên Ox nên tọa độ điểm H là H(2; 0) suy CH = 2 cm.

• Độ dài AB bằng: 6 – 1 = 5 (cm).

• Độ dài BH bằng: 2 – 1 = 1 (cm).

• Độ dài AH bằng: 6 – 2 = 4 (cm).

Áp dụng định lý Pythagore, ta có:

• AC² = AH² + CH² = 4² + 2² = 20.

Suy ra $A C = \sqrt{20}$ cm.

• BC² = BH² + CH² = 1² + 2² = 5.

Suy ra $B C = \sqrt{5}$ cm.

Khi đó, chu vi tam giác ABC là:

$A B + B C + A C = 5 + \sqrt{5} + \sqrt{20} \approx 11,71$ (cm)

Diện tích tam giác ABC là:

$\frac{1}{2} A B . C H = \frac{1}{2} . 5 . 2 = 5$ (cm²).

Vậy chu vi tam giác ABC khoảng 11, 71 cm và diện tích của tam giác ABC bằng 5 cm².

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán 8 Cánh diều

Bài 4 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Xem thêm lời giải bài tập Toán lớp 8 Cánh diều hay, chi tiết khác: