Giải Toán 8 trang 65 Tập 2 Cánh diều

---

Với Giải Toán 8 trang 65 Tập 2 trong Bài 3: Đường trung bình của tam giác Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 65.

Giải Toán 8 trang 65 Tập 2 Cánh diều

Bài 1 trang 65 Toán 8 Tập 2: Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thoả mãn MN // BC. Chứng minh NA = NC và $\mathrm{MN}=\frac{1}{2}\mathrm{BC}.$

Lời giải:

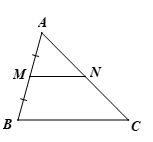
Xét ∆ABCvới MN // BC, ta có: $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$ (định lí Thalès)

Mà AM = MB (do M là trung điểm của AB) nên AN = NC.

Xét ∆ABCvới MN // BC, ta có: $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{MN}}{\mathrm{BC}}$ (hệ quả của định lí Thalès)

Mà $\mathrm{AM}=\frac{1}{2}\mathrm{AB}$ (do M là trung điềm của AB)

Suy ra $\mathrm{MN}=\frac{1}{2}\mathrm{BC}.$

Bài 2 trang 65 Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:

a) MN // CP;

b) AQ = QM;

c) CP = 4PQ.

Lời giải:

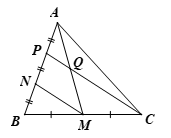
a) Do PN = NB nên N là trung điểm của BP.

Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.

Xét ∆BCP có M, N lần lượt là trung điểm của BC, BP nên MN là đường trung bình của ∆BCP

Suy ra MN // CP.

b) Do AP = PN nên P là trung điểm của AN.

Mà MN // CP, Q ∈ CP nên MN // PQ.

Xét ∆AMN có PQ đi qua P là trung điểm của AN và PQ // MN

Suy ra Q là trung điểm của AM nên AQ = QM.

c) Xét ∆AMN có P, Q lần lượt là trung điểm của AN, AM nên là đường trung bình của ∆AMN. Do đó $\mathrm{PQ}=\frac{1}{2}\mathrm{MN}.$

Lại có MN là đường trung bình của ∆BCP nên $\mathrm{MN}=\frac{1}{2}\mathrm{CP}.$

Khi đó $\mathrm{PQ}=\frac{1}{2}\mathrm{MN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{CP}=\frac{1}{4}\mathrm{CP}$

Suy ra CP = 4PQ.

Bài 3 trang 65 Toán 8 Tập 2: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

c) Cho AC ⊥ BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải:

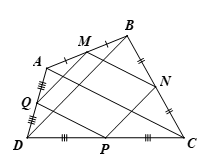
a) Xét ∆ABC có M, N lần lượt là trung điểm AB, BC nên MN là đường trung bình của ∆ABC

Suy ra MN//AC và $\mathrm{MN}=\frac{1}{2}\mathrm{AC}$ (1)

Xét ∆ADC có P, Q lần lượt là trung điểm DC, AD nên PQ là đường trung bình của ∆ADC

Suy ra PQ//AC và $\mathrm{PQ}=\frac{1}{2}\mathrm{AC}$ (2)

Từ (1) và (2) suy ra MN // PQ; MN = PQ.

Tứ giác MNPQ có MN // PQ; MN = PQ nên MNPQ là hình bình hành.

b) Xét tam giác ABD có M, Q lần lượt là trung điểm AB, AD nên MQ là đường trung bình của ∆ABD

Suy raMQ // BD và $\mathrm{MQ}=\frac{1}{2}\mathrm{BD}$

Mà $\mathrm{MN}=\frac{1}{2}\mathrm{AC}$ và AC = BD nên MN = MQ.

Hình bình hành MNPQ có MN = MQ nên MNPQ là hình thoi.

c) Ta có MN // AC (câu a), MQ // BD (câu b) và AC ⊥ BD (giả thiết)

Suy ra MN ⊥ MQ hay $\widehat{\mathrm{NMQ}}=90°$

Hình bình hành MNPQ có $\widehat{\mathrm{NMQ}}=90°$ nên là hình chữ nhật.

Bài 4 trang 65 Toán 8 Tập 2: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải:

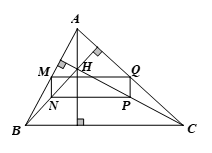
⦁Xét ∆ABH có M, N lần lượt là trung điểm của AB, BH nên MN là đường trung bình ∆ABH.

Suy ra MN//AH (1)

Tương tự, xét ∆AHC ta cũng có PQ là đường trung bình ∆AHC nên PQ//AH (2)

Từ (1) và (2) ta có MN // PQ // AH.

⦁ Chứng minh tương tự như trên với ∆ABC và ∆HBC, ta cũng có MQ, NP lần lượt là đường trung bình của ∆ABC và ∆HBC.

Do đó MQ // BC và NP // BC. Suy ra MQ // NP // BC.

Tứ giác MNPQ có MN // PQ và MQ // NP nên MNPQ là hình bình hành.

⦁ Ta có MN//AH và AH ⊥ BC (do H là trực tâm của ∆ABC) nên MN ⊥ BC

Lại có NP // BC nên suy ra MN ⊥ NP hay $\widehat{\mathrm{MNP}}=90°.$

Hình bình hành MNPQ có $\widehat{\mathrm{MNP}}=90°.$ nên MNPQ là hình chữ nhật.

Bài 5 trang 65 Toán 8 Tập 2: Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số và số , từ đó ước lượng được độ dài đoạn thẳng MN khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC. Hỏi khoảng cách đó khoảng bao nhiêu mét?

Lời giải:

Xét ∆ABC có MN là đường trung bình của ∆ABC nên $\mathrm{MN}=\frac{1}{2}\mathrm{BC}$

Suy ra BC = 2MN = 2.4,5 = 9(m).

Vậy khoảng cách giữa hai mép dưới của mái khoảng 9 m.

Lời giải bài tập Toán 8 Bài 3: Đường trung bình của tam giác hay khác:

• Giải Toán 8 trang 62