Giải Toán 8 trang 73 Tập 2 Cánh diều

---

Với Giải Toán 8 trang 73 Tập 2 trong Bài 5: Tam giác đồng dạng Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 73.

Giải Toán 8 trang 73 Tập 2 Cánh diều

Bài 1 trang 73 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP và $\hat{A}=45°,\hat{B}=60°.$Tính các góc C, M, N, P.

Lời giải:

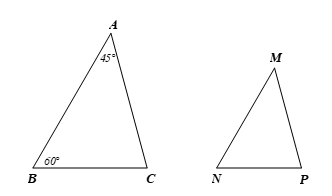
Xét ∆ABC ta có $\hat{A}+\hat{B}+\hat{C}=180°$ (tổng ba góc của một tam giác)

Suy ra $\hat{C}=180°-\hat{A}-\hat{B}=180°-45°-60°=75°.$

Vì ∆ABC ᔕ ∆MNP nên

$\hat{A}=\hat{M}=45°;\hat{B}=\hat{N}=60°;\hat{C}=\hat{P}=75°.$

Vậy $\hat{C}=\hat{P}=75°;\hat{M}=45°;\hat{N}=60°.$

Bài 2 trang 73 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP và AB = 4, BC = 6, CA = 5, MN = 5. Tính độ dài các cạnh NP, PM.

Lời giải:

Vì ∆ABC ᔕ∆MNPnên $\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{\mathrm{BC}}{\mathrm{NP}}=\frac{\mathrm{CA}}{\mathrm{PM}}$

Mà AB = 4 và MN = 5 nên $\frac{\mathrm{BC}}{\mathrm{NP}}=\frac{\mathrm{CA}}{\mathrm{PM}}=\frac{\mathrm{AB}}{\mathrm{MN}}=\frac{4}{5}$

Do vậy: $\mathrm{NP}=\frac{5}{4}\mathrm{BC}=\frac{5}{4}\cdot 6=\frac{15}{2};\mathrm{PM}=\frac{5}{4}\mathrm{CA}=\frac{5}{4}\cdot 5=\frac{25}{4}.$

Vậy $\mathrm{NP}=\frac{15}{2};\mathrm{PM}=\frac{25}{4}.$

Bài 3 trang 73 Toán 8 Tập 2: Ba vị trí A, B, C trong thực tiễn lần lượt được mô tả bởi ba đỉnh của tam giác A’B’C’ trên bản vẽ. Biết tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số $\frac{1}{1000000}$ và A’B’ = 4 cm, B’C’ = 5 cm, C’A’ = 6 cm. Tính khoảng cách giữa hai vị trí A và B, B và C, C và A trong thực tiễn (theo đơn vị kilômét).

Lời giải:

Đổi đơn vị:

A’B’ = 4 cm = 0,00004 km;

B’C’ = 5 cm = 0,00005 km;

C’A’ = 6 cm = 0,00006 km.

Vì ∆A’B’C’ đồng dạng với ∆ABCtheo tỉ số $\frac{1}{1000000}$ nên ta có:

$\frac{A^{\text{'}}{B}^{\text{'}}}{\mathrm{AB}}=\frac{A^{\text{'}}{C}^{\text{'}}}{\mathrm{AC}}=\frac{B^{\text{'}}{C}^{\text{'}}}{\mathrm{BC}}=\frac{1}{1000000}$

Do vậy khoảng cách giữa hai vị trí A và B, B và C, C và A trong thực tiễn là:

AB = 0,00004 . 1 000 000 = 40 (km);

BC = 0,00005 . 1 000 000 = 50 (km);

AB = 0,00006 . 1 000 000 = 60 (km).

Bài 4 trang 73 Toán 8 Tập 2: Trong Hình 54, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí C, D. Giả sử chọn được các vị trí A, B, E sao cho ∆ABE ᔕ ∆ACD và đo được AB = 20 m, AC = 50 m, BE = 8 m. Tính độ rộng của khúc sông đó.

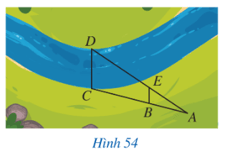
Lời giải:

Vì ∆ABE ᔕ ∆ACD nên $\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BE}}{\mathrm{CD}}=\frac{\mathrm{EA}}{\mathrm{DA}}$

Mà AB = 20m, AC = 50 m nên ta có $\frac{\mathrm{BE}}{\mathrm{CD}}=\frac{\mathrm{EA}}{\mathrm{DA}}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{20}{50}=\frac{2}{5}$

Do vậy độ rộng của khúc sông đó là CD là: $\mathrm{CD}=\frac{5}{2}\mathrm{BE}=\frac{5}{2}\cdot 8=20$(m).

Bài 5 trang 73 Toán 8 Tập 2: Cho tam giác ABC (Hình 55), các điểm M, N thuộc cạnh AB thoả mãn AM = MN = NB, các điểm P, Q thuộc cạnh AC thoả mãn AP = PQ = QC. Tam giác AMP đồng dạng với những tam giác nào?

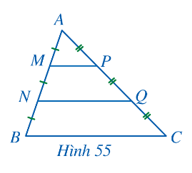
Lời giải:

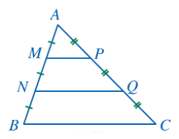
Vì AM = MN; AP = PQ nên M, P lần lượt là trung điểm của AN, AQ.

Xét ∆ANQ có M, P lần lượt là trung điểm của AN, AQ nên MP là đường trung bình của ∆ANQ.

Suy ra MP // NQ nên ∆AMP ᔕ ∆ANQ.

Do AM = MN = NB; AP = PQ = QC nên ta có $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AP}}{\mathrm{AC}}=\frac{1}{3}$

Xét ∆ABC có $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AP}}{\mathrm{AC}}$ nên MP // BC (định lí Pythagore đảo)

Do đó ∆AMP ᔕ ∆ABC.

Bài 6 trang 73 Toán 8 Tập 2: Cho hình bình hành ABCD. Một đường thẳng đi qua D lần lượt cắt đoạn thẳng BC và tia AB tại M và N sao cho điểm M nằm giữa hai điểm B và C. Chứng minh:

a) ∆NBM ᔕ ∆NAD;

b) ∆NBM ᔕ ∆DCM;

c) ∆NAD ᔕ ∆DCM.

Lời giải:

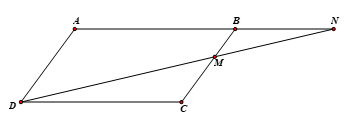
a) Do ABCD là hình bình hành nên BC // AD hay BM // AD.

Do BM // AD nên ∆NBM ᔕ ∆NAD.

b) Do ABCD là hình bình hành nên AB // CD hay BN // CD.

Do BN // CD nên ∆NBM ᔕ ∆DCM.

c) Do ∆NBM ᔕ ∆NAD nên ∆NAD ᔕ ∆NBM

Mà ∆NBM ᔕ ∆DCM nên ∆NAD ᔕ ∆DCM.

Lời giải bài tập Toán 8 Bài 5: Tam giác đồng dạng hay khác:

• Giải Toán 8 trang 70

• Giải Toán 8 trang 71

• Giải Toán 8 trang 72