Bài 6 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

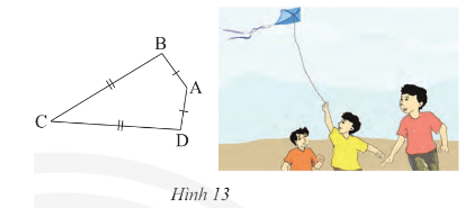
Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 6 trang 67 Toán 8 Tập 1: Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

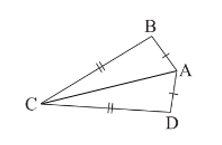
a) Chứng minh rằng AC là đường trung trực của BD.

b) Cho biết $\hat{B} = 95 °$ , $\hat{C} = 35 °$ . Tính $\hat{A}$ và $\hat{D}$ .

Bài 6 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Lời giải:

Bài 6 trang 67 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.

Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.

Do đó AC là đường trung trực của đoạn thẳng BD.

b) Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\hat{B} = \hat{D}$ (hai góc tương ứng).

Mà $\hat{B} = 95 °$ nên $\hat{D} = 95 °$ .

Xét tứ giác ABCD có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ (định lí tổng các góc của một tứ giác)

Suy ra $\hat{A} = 360 ° - (\hat{B} + \hat{C} + \hat{D})$

Do đó $\hat{A} = 360 ° - (95 ° + 35 ° + 95 °) = 135 °$ .

Vậy $\hat{A} = 135 °$ và $\hat{D} = 95 °$ .

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác: