Giải Toán 8 trang 20 Tập 2 Chân trời sáng tạo

---

Với Giải Toán 8 trang 20 Tập 2 trong Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0) Toán lớp 8 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 20.

Giải Toán 8 trang 20 Tập 2 Chân trời sáng tạo

Thực hành 3 trang 20 Toán 8 Tập 2: a) Vẽ đồ thị của các hàm số: y = 0,5x; y = −3x; y = x.

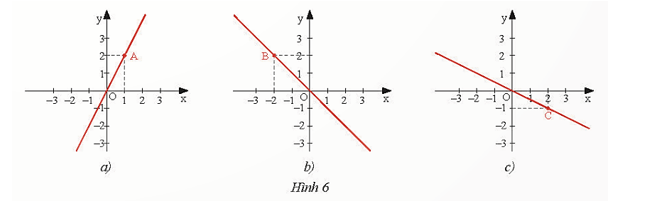
b) Các đồ thị sau đây là đồ thị của hàm số nào?

Lời giải:

a)

+) Đồ thị y = 0,5x

Cho x = 2 ta có y = 1. Ta vẽ điểm A (2; 1).

Đồ thị hàm số y = 0,5x là đường thẳng đi qua các điểm O(0; 0) và A(2; 1).

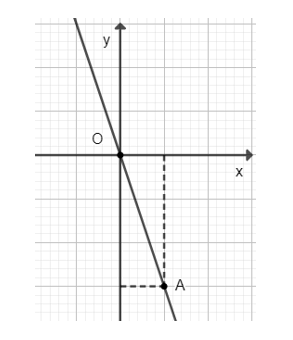
+) Đồ thị y = −3x

Cho x = 1 ta có y = −3. Ta vẽ điểm B (1; −3),

Đồ thị hàm số y = −3x là đường thẳng đi qua các điểm O(0; 0) và A(1; −3),

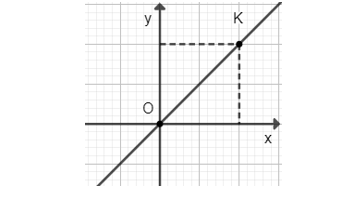
+) Đồ thị y = x

Cho x = 2 ta có y = 2. Ta vẽ điểm K (2; 2).

Đồ thị hàm số y = x là đường thẳng đi qua các điểm O(0; 0) và K(2; 2).

b)

+) Đồ thị Hình 6a) đi qua A(1; 2) và O(0; 0) suy ra đây là đồ thị hàm số y = 2x.

+) Đồ thị Hình 6b) đi qua B(−2; 2) và O(0; 0) suy ra đây là đồ thị của hàm số y = −x.

+) Đồ thị Hình 6c) đi qua C(2; −1) và O(0; 0) suy ra đây là đồ thị của hàm số

y = −0,5x.

Khám phá 4 trang 20 Toán 8 Tập 2: Cho hai hàm số y = f(x) = x và y = g(x) = x + 3.

a) Thay dấu ? bằng số thích hợp

b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị hàm số y = f(x) và biều diễn các điểm có tọa độ thỏa mãn hàm số y = g(x) có trong bảng trên.

c) Kiểm tra xem các điểm thuộc đồ thị hàm số y = g(x) vẽ ở câu b có thẳng hàng không? Và dự đoán cách vẽ đồ thị của hàm số y = g(x).

Lời giải:

a)

 

b) Đồ thị hàm số y = f(x) đi qua điểm O(0; 0) và điểm có tọa độ A(1; 1).

Đồ thị hàm số y = f(x) đi qua điểm B(−2; 1), C(−1; 2), D(0; 3), E(1; 4), F(2; 5).

c) Các điểm thuộc đồ thị hàm số y = g(x) thẳng hàng với nhau nên đồ thị hàm số

y = g(x) song song với đồ thị hàm số y = f(x).

Lời giải bài tập Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0) Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 16
• Giải Toán 8 trang 17
• Giải Toán 8 trang 18
• Giải Toán 8 trang 21
• Giải Toán 8 trang 22