Giải Toán 8 trang 23 Tập 2 Chân trời sáng tạo
Với Giải Toán 8 trang 23 Tập 2 trong Bài 4: Hệ số góc của đường thẳng Toán lớp 8 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 23.
Giải Toán 8 trang 23 Tập 2 Chân trời sáng tạo
Khởi động trang 23 Toán 8 Tập 2: Khi nào thì hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b (a’ ≠ 0) song song với nhau, trùng nhau, cắt nhau?
Lời giải:
+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0 ) song song với nhau khi a = a’ và b ≠ b’.
+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0) cắt nhau khi a ≠ a’
+) Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’(a’ ≠ 0) trùng nhau khi a = a’ và b = b’.
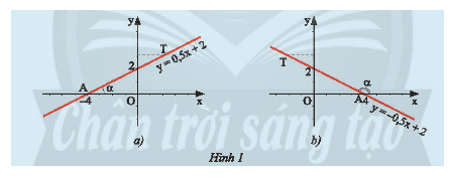
Khám phá 1 trang 23 Toán 8 Tập 2: a) Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0) cắt Ox tại điểm A và T là một điểm trên đường thẳng y = ax + b (a ≠ 0) có tung độ dương (Hình 1).
Ta gọi là góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox. Nêu nhận xét của em về số đo của góc α và hệ số a trong hai trường hợp dưới đây.
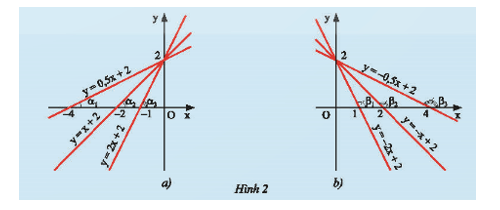
b) Hãy so sánh các hệ số a của các đường thẳng y = ax + b trong mỗi hình ở Hình 2 và so sánh các góc α hoặc các góc β tạo bởi các đường thẳng đó với trục Ox.
Lời giải:
a) Khi a > 0 thì góc α là góc nhọn.
Khi a < 0 thì góc α là góc tù.
b) Với hệ số a dương, hệ số a càng lớn thì góc α càng lớn.
Với hế số a âm, hệ số a càng lớn thì góc β càng lớn.
Lời giải bài tập Toán 8 Bài 4: Hệ số góc của đường thẳng Chân trời sáng tạo hay khác: