Giải Toán 8 trang 25 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 25 Tập 1 trong Bài 4: Phân tích đa thức thành nhân tử Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 25.

Giải Toán 8 trang 25 Tập 1 Chân trời sáng tạo

Thực hành 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) a³ – a²b + a – b;

b) x² – y² + 2y – 1.

Lời giải:

a) a³ – a²b + a – b

= (a³ – a²b) + (a – b)

= a²(a – b) + (a – b)

= (a – b)(a² + 1).

b) x² – y² + 2y – 1

= x² – (y² – 2y + 1)

= x² – (y – 1)²

= (x + y – 1).[x – (y – 1)]

= (x + y – 1)(x – y + 1).

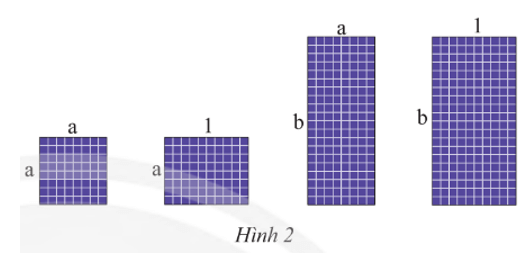
Vận dụng 3 trang 25 Toán 8 Tập 1: Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).

Lời giải:

Diện tích tấm pin hình vuông có cạnh bằng a là: a² (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng 1 và chiều rộng bằng a là: a.1 = a (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng a là: ab (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng 1 là: b.1 = b (m²).

Tổng diện tích bốn tấm pin mặt trời là:

S = a² + a + ab + b = (a² + a) + (ab + b)

                               = a(a + 1) + b(a + 1)

                               = (a + 1)(a + b) (m²).

Vậy có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật có chiều rộng là a + 1 (m) và chiều dài là a + b (m).

Với a = 0,8 (m) và b = 2 (m) ta có:

• Chiều rộng hình chữ nhật đó là 0,8 + 1 = 1,8 (m).

• Chiều dài hình chữ nhật đó là 0,8 + 2 = 2,8 (m).

• Diện tích hình chữ nhật đó là: 1,8 . 2,8 = 5,04 (m²).

Bài 1 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x³ + 4x;

b) 6ab – 9ab²;

c) 2a(x – 1) + 3b(1 – x);

d) (x – y)² – x(y – x).

Lời giải:

a) x³ + 4x = x.x² + x.4 = x(x² + 4).

b) 6ab – 9ab² = 3ab.2 – 3ab.3b = 3ab(2 – 3b).

c) 2a(x – 1) + 3b(1 – x)

= 2a(x – 1) + 3b[– (x – 1)]

= 2a(x – 1) – 3b(x – 1)

= (x – 1)(2a – 3b).

d) (x – y)² – x(y – x)

= (x – y)² + x(x – y)

= (x – y)(x – y + x)

= (x – y)(2x – y).

Bài 2 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x² – 1;

b) (x + 2)² – 9;

c) (a + b)² – (a – 2b)².

Lời giải:

a) 4x² – 1 = (2x)² – 1² = (2x + 1)(2x –1).

b) (x + 2)² – 9 = (x + 2)² – 3²

                       = (x + 2 + 3)(x + 2 – 3)

                       = (x + 5)(x – 1).

c) (a + b)² – (a – 2b)²

= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]

= [a + b + a – 2b] . [a + b – a + 2b]

= (2a – b).3b.

Bài 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4a² + 4a + 1;

b) –3x² + 6xy – 3y²;

c) (x + y)² – 2(x + y)z + z².

Lời giải:

a) 4a² + 4a + 1

= (2a)² + 2.2a.1 + 1²

= (2a + 1)².

b) –3x² + 6xy – 3y²

= –3(x² – 2xy + y²)

= –3(x – y)².

c) (x + y)² – 2(x + y)z + z²

= [(x + y) – z]²

= (x + y – z)².

Bài 4 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 8x³ – 1;

b) x³ + 27y³;

c) x³ – y⁶.

Lời giải:

a) 8x³ – 1

= (2x)³ – 1³

= (2x – 1)[(2x)² + 2x.1 + 1²]

= (2x – 1)(4x² + 2x + 1).

b) x³ + 27y³

= x³ + (3y)³

= (x + 3y)[x² – x.3y + (3y)²]

= (x + 3y)(x² – 3xy + 9y²).

c) x³ – y⁶

= x³ – (y²)³

= (x – y²)[x² + x.y² + (y²)²]

= (x – y²)(x² + xy² + y⁴).

Bài 5 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x³ – 16x;

b) x⁴ – y⁴;

c) xy² + x²y + $\frac{1}{4}$y³;

d) x² + 2x – y² + 1.

Lời giải:

a) 4x³ – 16x

= 4x(x² – 4)

= 4x(x² – 2²)

= 4x(x + 2)(x – 2).

b) x⁴ – y⁴

= (x²)² – (y²)²

= (x² + y²)(x² – y²)

= (x² + y²)(x + y)(x – y).

c) xy² + x²y + $\frac{1}{4}$y³

= y(xy + x² + $\frac{1}{4}$y²)

$=y\left[x^2+2.x.\frac{1}{2}y+{\left(\frac{1}{2}y\right)}^2\right]$

$=y{\left(x+\frac{1}{2}y\right)}^2$.

d) x² + 2x – y² + 1

= (x² + 2x + 1) – y²

= (x + 1)² – y²

= (x + 1 + y)(x + 1 – y).

Bài 6 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – xy + x – y;

b) x² + 2xy – 4x – 8y;

c) x³ – x² – x + 1.

Lời giải:

a) x² – xy + x – y

= (x² – xy) + (x – y)

= x(x – y) + (x – y)

= (x – y)(x + 1).

b) x² + 2xy – 4x – 8y

= (x² + 2xy) – (4x + 8y)

= x(x +  2y) – 4(x + 2y)

= (x +  2y)(x – 4).

c) x³ – x² – x + 1

= (x³ – x²) – (x – 1)

= x²(x – 1) – (x – 1)

= (x – 1)(x² – 1)

= (x – 1)(x + 1)(x – 1)

= (x – 1)²(x + 1).

Bài 7 trang 25 Toán 8 Tập 1: Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4.

Lời giải:

Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a².

Tức là 49y² + 28y + 4 = a².

Ta phân tích đa thức 49y² + 28y + 4 thành nhân tử có dạng a².

49y² + 28y + 4

= (7y)² + 2.7y.2 + 2²

= (7y + 2)²

Vậy độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4 là 7y + 2.

Lời giải bài tập Toán 8 Bài 4: Phân tích đa thức thành nhân tử Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 23

• Giải Toán 8 trang 24