Giải Toán 8 trang 78 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 78 Tập 1 trong Bài 4: Hình bình hành – Hình thoi Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 78.

Giải Toán 8 trang 78 Tập 1 Chân trời sáng tạo

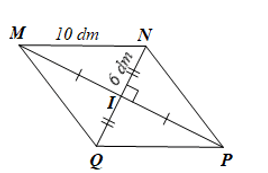
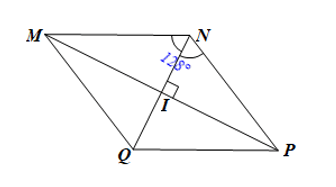
Thực hành 3 trang 78 Toán 8 Tập 1: Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.

a) Tính MP khi biết MN = 10 dm, IN = 6 dm.

b) Tính $\widehat{IMN}$ khi biết $\widehat{MNP}=128°$.   

Lời giải:

a)

Do MNPQ là hình thoi nên hai đường chéo MP và NQ vuông góc với nhau tại trung điểm của mỗi đường.

Áp dụng định lí Pythagore vào DMNI vuông tại I, ta có:

MN² = MI² + NI²

Suy ra $MI=\sqrt{M{N}^2-N{I}^2}=\sqrt{{10}^2-6^2}=8$ (dm).

Do I là trung điểm của MP nên MP = 2MI = 2.8 = 16 (dm).

Vậy MP = 16 dm.

b)

Vì MNPQ là hình thoi nên MQ // NP

Do đó $\widehat{MNP}+\widehat{NMQ}=180°$

Suy ra $\widehat{NMQ}=180°-\widehat{MNP}=180°-128°=52°$.

Do MNPQ là hình thoi nên MP và tia phân giác của góc NMQ.

Suy ra $\widehat{IMN}=\frac{1}{2}\widehat{NMQ}=\frac{1}{2}.52°=26°$.

Vậy $\widehat{IMN}=26°$.

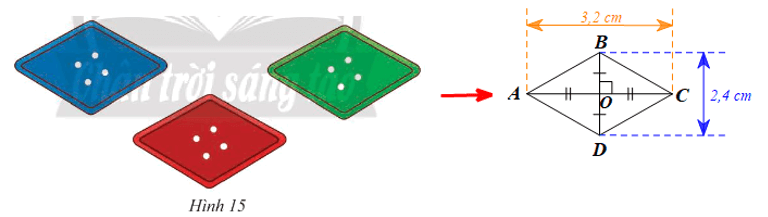
Vận dụng 4 trang 78 Toán 8 Tập 1: Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là 3,2 cm và 2,4 cm.

Lời giải:

Hình ảnh chiếc khuy áo được vẽ lại bởi hình thoi ABCD như hình vẽ trên.

Gọi O là giao điểm của hai đường chéo AC và BD.

Khi đó hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra OA = $\frac{1}{2}$AC = 1,6 cm và OB = $\frac{1}{2}$BD = 1,2 cm.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB²

Suy ra $AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{1,6^2+1,2^2}=2$ (cm).

Vậy độ dài cạnh của khuy áo là 2 cm.

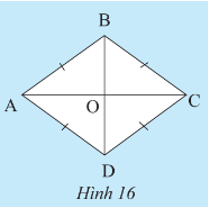
Khám phá 6 trang 78 Toán 8 Tập 1: Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau:

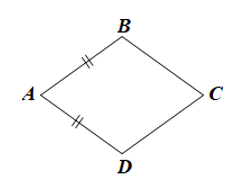
Trường hợp 1: AB = AD.

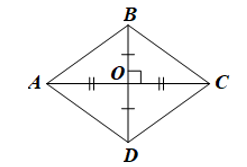
Trường hợp 2: AC vuông góc với BD.

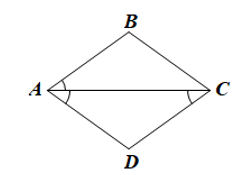
Trường hợp 3: AC là phân giác góc BAD.

Trường hợp 4: BD là phân giác góc ABC.

Lời giải:

• Trường hợp 1: AB = AD.

Vì ABCD là hình bình hành nên AD = BC và AB = CD.

Lại có AB = AD (giả thiết)

Do đó AB = AD = BC = CD.

• Trường hợp 2: AC vuông góc với BD.

Vì ABCD là hình bình hành nên AD = BC, AB = CD và hai đường chéo AC, BD cắt nhau tại trung điểm O của mỗi đường.

Xét DOAB và DOCB có:

$\widehat{AOB}=\widehat{COB}=90°$; OB là cạnh chung; OA = OC

Do đó DOAB = DOCB (hai cạnh góc vuông)

Suy ra AB = CB (hai cạnh tương ứng).

Mà AD = BC và AB = CD nên AB = CD = CB = DA.

• Trường hợp 3: AC là phân giác góc BAD.

Vì ABCD là hình bình hành nên AB // CD

Do đó $\widehat{BAC}=\widehat{CDA}$ (so le trong).

Mà $\widehat{BAC}=\widehat{CAD}$ (do AC là tia phân giác của góc BAD)

Suy ra $\widehat{CAD}=\widehat{CDA}$.

Tam giác ACD có $\widehat{CAD}=\widehat{CDA}$ nên là tam giác cân tại D

Suy ra DA = DC.

Lại có AB = CD và AD = BC (chứng minh trên).

Do đó AB = BC = CD = DA.

• Trường hợp 4: BD là phân giác góc ABC.

Chứng minh tương tự như trường hợp 3 ta cũng có AB = BC = CD = DA.

Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 73

• Giải Toán 8 trang 74

• Giải Toán 8 trang 76

• Giải Toán 8 trang 79

• Giải Toán 8 trang 80

• Giải Toán 8 trang 81