Giải Toán 9 trang 66 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 66 Tập 2 trong Bài tập cuối chương 7 Toán 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 66.

Giải Toán 9 trang 66 Tập 2 Cánh diều

Bài 1 trang 66 Toán 9 Tập 2: Cho phương trình x² + 2x + c = 0. Điều kiện của c để phương trình có hai nghiệm phân biệt là

A. c < 1.

B. c > 1.

C. c ≤ 1.

D. c ≥ 1.

Lời giải:

Đáp án đúng là: A

Phương trình x² + 2x + c = 0 có các hệ số a = 1, b = 2 và c.

Do b = 2 nên b’ = 1.

Ta có: ∆’ = 1² – 1.c = 1 – c.

Để phương trình x² + 2x + c = 0 có hai nghiệm phân biệt thì ∆’ > 0, tức là 1 – c > 0, suy ra c < 1.

Vậy ta chọn phương án A.

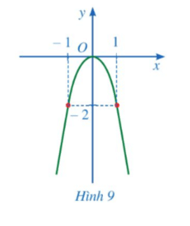
Bài 2 trang 66 Toán 9 Tập 2: Giả sử đồ thị của hàm số y = ax² là parabol ở Hình 9. Giá trị của a bằng

A. 2.

B. –2.

C. $\frac{1}{2}.$

D. $-\frac{1}{2}.$

Lời giải:

Đáp án đúng là: B

Quan sát Hình 9 ta thấy đồ thị hàm số đi qua điểm (1; –2) nên thay x = 1 và y = –2 vào hàm số y = ax², ta có:

–2 = a.1² hay a = –2.

Vậy ta chọn phương án B.

Bài 3 trang 66 Toán 9 Tập 2: Cho hàm số $y=-\frac{2}{3}{x}^2.$

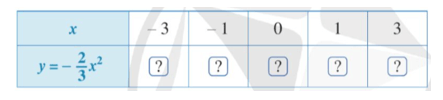
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số.

Lời giải:

a) Xét hàm số $y=-\frac{2}{3}{x}^2.$

Với x = –3 thì $y=-\frac{2}{3}\cdot {\left(-3\right)}^2=-6;$

Với x = –1 thì $y=-\frac{2}{3}\cdot {\left(-1\right)}^2=-\frac{2}{3};$

Với x = 0 thì $y=-\frac{2}{3}\cdot 0^2=0;$

Với x = 1 thì $y=-\frac{2}{3}\cdot 1^2=-\frac{2}{3};$

Với x = 3 thì $y=-\frac{2}{3}\cdot 3^2=-6.$

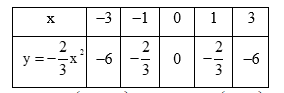
Vậy ta hoàn thành được bảng giá trị như sau:

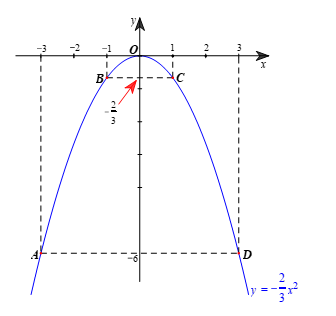
b) – Vẽ các điểm A(–3; –6); $B\left(-1;-\frac{2}{3}\right);$ O(0; 0); $C\left(1;-\frac{2}{3}\right);$ D(3; –6) thuộc đồ thị hàm số $y=-\frac{2}{3}{x}^2$ trong mặt phẳng tọa độ Oxy.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số $y=-\frac{2}{3}{x}^2$ (hình vẽ).

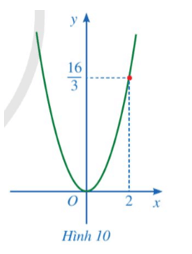
Bài 4 trang 66 Toán 9 Tập 2: Trong mặt phẳng toạ độ Oxy, đường parabol ở Hình 10 biểu diễn đồ thị của hàm số y = ax².

a) Tìm hệ số a.

b) Tìm điểm thuộc đồ thị có hoành độ bằng 3.

c) Tìm điểm thuộc đồ thị có tung độ bằng 4.

Lời giải:

a) Quan sát Hình 10, ta thấy đồ thị hàm số y = ax² đi qua điểm $\left(2;\frac{16}{3}\right)$nên thay x = 2 và $y=\frac{16}{3}$ vào hàm số y = ax², ta được: $\frac{16}{3}=a\cdot 2^2,$ hay $4a=\frac{16}{3},$ suy ra $a=\frac{4}{3}.$

Vậy $a=\frac{4}{3}.$

b) Khi $a=\frac{4}{3},$ ta có hàm số $y=\frac{4}{3}{x}^2.$

Điểm thuộc đồ thị $y=\frac{4}{3}{x}^2$ có hoành độ bằng 3 nên thay x = 3 vào hàm số $y=\frac{4}{3}{x}^2,$ ta được: $y=\frac{4}{3}\cdot 3^2=12.$

Vậy điểm cần tìm là (3; 12).

c) Điểm thuộc đồ thị $y=\frac{4}{3}{x}^2$ có tung độ bằng 4 nên thay y = 4 vào hàm số $y=\frac{4}{3}{x}^2,$ ta được: $4=\frac{4}{3}{x}^2,$ suy ra $x^2=3,$ nên $x=\sqrt{3}$ hoặc $x=-\sqrt{3}.$

Vậy các điểm cần tìm là $\left(\sqrt{3};4\right)$và $\left(-\sqrt{3};4\right).$

Bài 5 trang 66 Toán 9 Tập 2: Giải các phương trình:

a) 3x² – 2x – 4 = 0;

b) 9x² – 24x + 16 = 0;

c) $2x^2+x+\sqrt{2}=0.$

Lời giải:

a) 3x² – 2x – 4 = 0

Phương trình có các hệ số a = 3, b = –2, c = –4. Do b = –2 nên b’ = –1.

Ta có: ∆’ = (–1)² – 3.(–4) = 13 > 0.

Do ∆’ > 0 nên phương trình đã cho có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-1\right)+\sqrt{13}}{3}=\frac{1+\sqrt{13}}{3};$$x_2=\frac{-\left(-1\right)-\sqrt{13}}{3}=\frac{1-\sqrt{13}}{3}.$

b) 9x² – 24x + 16 = 0

Phương trình có các hệ số a = 9, b = –24, c = 16. Do b = –24 nên b’ = –12.

Ta có: ∆’ = (–12)² – 9.16 = 0.

Do ∆’ = 0 nên phương trình đã cho có nghiệm kép $x_1=x_2=-\frac{-12}{9}=\frac{4}{3}.$

c) $2x^2+x+\sqrt{2}=0$

Phương trình có các hệ số a = 2, b = 1, c = $\sqrt{2},$

$\Delta =1^2-4\cdot 2\cdot \sqrt{2}=1-8\sqrt{2}<0.$

Do ∆ < 0 nên phương trình đã cho vô nghiệm.

Bài 6 trang 66 Toán 9 Tập 2: Không tính ∆, giải các phương trình:

a) x² – 3x + 2 = 0;

b) –3x² + 5x + 8 = 0;

c) $\frac{1}{3}{x}^2+\frac{1}{6}x-\frac{1}{2}=0.$

Lời giải:

a) x² – 3x + 2 = 0

Phương trình có các hệ số a = 1, b = –3, c = 2.

Ta thấy: a + b + c = 1 + (–3) + 2 = 0.

Do đó phương trình đã cho có nghiệm x₁ = 1 và $x_2=\frac{2}{1}=2.$

b) –3x² + 5x + 8 = 0

Phương trình có các hệ số a = –3, b = 5, c = 8.

Ta thấy: a – b + c = –3 – 5 + 8 = 0.

Do đó phương trình đã cho có nghiệm x₁ = –1 và $x_2=-\frac{8}{-3}=\frac{8}{3}.$

b) $\frac{1}{3}{x}^2+\frac{1}{6}x-\frac{1}{2}=0$

Phương trình có các hệ số $b=\frac{1}{6};$$x=-\frac{1}{2}.$

Ta thấy:$a+b+c=\frac{1}{3}+\frac{1}{6}+\left(\frac{-1}{2}\right)=0.$

Do đó phương trình đã cho có nghiệm x­₁ = 1 và $x_2=\frac{-\frac{1}{2}}{\frac{1}{3}}=-\frac{3}{2}.$

Bài 7 trang 66 Toán 9 Tập 2: Tìm hai số, biết tổng của chúng bằng $4\sqrt{2}$ và tích của chúng bằng 6.

Lời giải:

Hai số cần tìm là nghiệm của phương trình $x^2-4\sqrt{2}x+6=0.$

Phương trình có các hệ số a = 1, $b=-4\sqrt{2},$ c = 6.

Do $b=-4\sqrt{2}$ nên $b^{\text{'}}=-2\sqrt{2}.$

Ta có: ${\Delta }^{\text{'}}={\left(-2\sqrt{2}\right)}^2-1\cdot 6=8-6=2>0.$

Do ∆’ > 0 nên phương trình đã cho có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-2\sqrt{2}\right)+\sqrt{2}}{1}=3\sqrt{2};$$x_2=\frac{-\left(-2\sqrt{2}\right)-\sqrt{2}}{1}=\sqrt{2}.$

Vậy hai số cần tìm là $3\sqrt{2}$và $\sqrt{2}$

Lời giải bài tập Toán 9 Bài tập cuối chương 7 hay khác:

• Giải Toán 9 trang 67