Giải Toán 9 trang 63 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 63 Tập 2 trong Bài 26: Xác suất của biến cố liên quan tới phép thử Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 63.

Giải Toán 9 trang 63 Tập 2 Kết nối tri thức

Luyện tập 3 trang 63 Toán 9 Tập 2: Trở lại Ví dụ 3, tính xác suất để cây con có hạt vàng và nhăn.

Lời giải:

Theo ví dụ 3, ta có không gian mẫu của phép thử là:

Ω = {AA, BB); (AA, Bb); (AA, bB); (AA, bb); (Aa, BB); (Aa, Bb); (Aa, bB); (Aa, bb)}.

Tập Ω có 8 phần tử. Phép thử có 8 kết quả có thể. Do cây con chọn ngẫu nhiên một gene từ cây bố và một gene từ cây mẹ nên các kết quả có thể trên là đổng khả năng.

Gọi M là biến cố “Cây con có hạt vàng và nhăn”.

Cây con có hạt vàng và nhăn nếu trong gene màu hạt có ít nhất một allele trội A và trong gene dạng hạt có cả hai allele lặn b.

Có 2 kết quả thuận lợi cho biến cố M là (AA, bb); (Aa, bb).

Vậy $P\left(M\right)=\frac{2}{8}=\frac{1}{4}.$

Bài 8.5 trang 63 Toán 9 Tập 2: Chọn ngẫu nhiên một gia đình có hai con. Giả thiết rằng biến cố “Sinh con trai” và biến cố “Sinh con gái” là đồng khả năng. Tính xác suất của các biến cố sau:

A: “Gia đình đó có cả con trai và con gái”;

B: “Gia đình đó có con trai”.

Lời giải:

Phép thử là chọn ngẫu nhiên một gia đình có hai con.

Kết quả của phép thử là (a, b), trong đó a và b tương ứng là giới tính của người con thứ nhất và người con thứ hai.

Không gian mẫu của phép thử là Ω = {(Trai, Trai); (Trai, Gái); (Gái, Trai); (Gái, Gái)}.

Tập Ω có 4 phần tử.

a) Có 2 kết quả thuận lợi cho biến cố A là: (Trai, Gái); (Gái, Trai).

Vậy $P\left(A\right)=\frac{2}{4}=\frac{1}{2}.$

b) Có 3 kết quả thuận lợi cho biến cố B là: (Trai, Trai); (Trai, Gái); (Gái, Trai).

Vậy $P\left(B\right)=\frac{3}{3}.$

Bài 8.6 trang 63 Toán 9 Tập 2: Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất các biến cố sau:

E: “Có đúng một con xúc xắc xuất hiện mặt 6 chấm”;

F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”;

G: “Tích của hai số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”.

Lời giải:

⦁ Phép thử là gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II.

Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số chấm xuất hiện trên con xúc xắc I và con xúc xắc II.

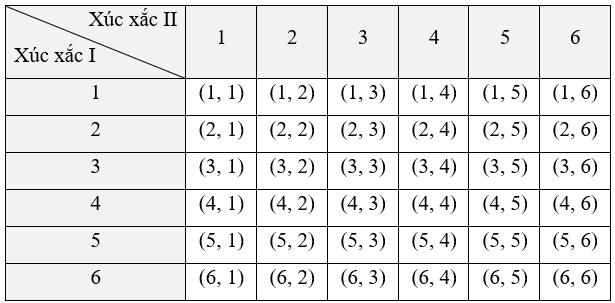
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (5, 6); (6, 6)}.

Tập Ω có 36 phần tử.

⦁ Có 10 kết quả thuận lợi cho biến cố E là: (1, 6); (2, 6); (3, 6); (4, 6); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5). Do đó $P\left(E\right)=\frac{10}{36}=\frac{5}{18}.$

⦁ Có 11 kết quả thuận lợi cho biến cố F là: (1, 6); (2, 6); (3, 6); (4, 6); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6). Do đó $P\left(F\right)=\frac{11}{36}.$

⦁ Có 14 kết quả thuận lợi cho biến cố G là: (1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (3, 1); (3, 2); (4, 1); (5, 1); (6, 1). Do đó $P\left(G\right)=\frac{14}{36}=\frac{7}{18}.$

Bài 8.7 trang 63 Toán 9 Tập 2: Bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1; 2; 3; 4; 5. Tính xác suất của các biến cố sau:

E: “Rút được tấm thẻ ghi số lẻ”;

F: “Rút được tấm thẻ ghi số chẵn và đồng xu xuất hiện mặt sấp”;

G: “Rút được tấm thẻ ghi số 5 hoặc đồng xu xuất hiện mặt ngửa”.

Lời giải:

⦁ Phép thử là bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1; 2; 3; 4; 5.

Kết quả của phép thử là (a, b), trong đó a và b tương ứng là mặt xuất hiện của đồng xu (mặt sấp (S), mặt ngửa (N)) và số ghi trên tấm thẻ.

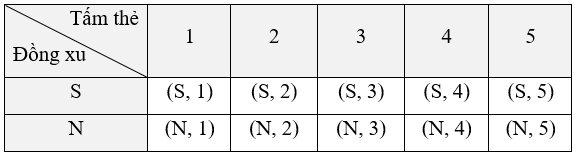
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 10 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(S, 1); (S, 2); (S, 3); (S, 4); (S, 5); (N, 1); (N, 2); (N, 3); (N, 4); (N, 5)}.

Tập Ω có 10 phần tử.

⦁ Có 6 kết quả thuận lợi cho biến cố E là: (S, 1); (S, 3); (S, 5); (N, 1); (N, 3); (N, 5). Do đó $P\left(E\right)=\frac{6}{10}=\frac{3}{5}.$

⦁ Có 2 kết quả thuận lợi cho biến cố F là: (S, 2); (S, 4). Do đó $P\left(F\right)=\frac{2}{10}=\frac{1}{5}.$

⦁ Có 6 kết quả thuận lợi cho biến cố G là: (S, 5); (N, 1); (N, 2); (N, 3); (N, 4); (N, 5). Do đó $P\left(G\right)=\frac{6}{10}=\frac{3}{5}.$

Bài 8.8 trang 63 Toán 9 Tập 2: Có hai túi I và II mỗi túi chứa 4 tấm thẻ được đánh số 1; 2; 3; 4. Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên hai tấm thẻ với nhau. Tính xác suất của các biến cố sau:

A: “Kết quả là một số lẻ”;

B: “Kết quả là 1 hoặc một số nguyên tố”.

Lời giải:

⦁ Phép thử là rút ngẫu nhiên từ mỗi túi ra một tấm thẻ.

Kết quả của phép thử là một cặp số (a, b), trong đó a và b tương ứng là số ghi trên thẻ được rút ra ở túi I và túi II.

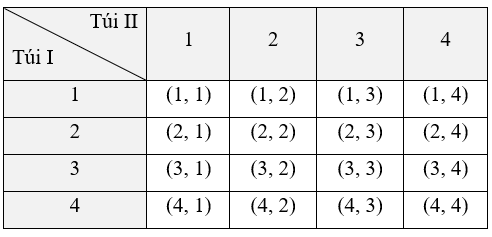
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô trong bảng là một kết quả có thể. Không gian mẫu là tập hợp 16 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); (1, 4); (2, 1); (2, 2); (2, 3); (2, 4); (3, 1); (3, 2); (3, 3); (3, 4); (4, 1); (4, 2); (4, 3); (4, 4)}.

Tập Ω có 16 phần tử.

⦁ Xét biến cố A: “Tích hai số ghi trên hai tấm thẻ là một số lẻ”.

Có 4 kết quả thuận lợi cho biến cố A là: (1, 1); (1, 3); (3, 1); (3, 3). Do đó $P\left(E\right)=\frac{4}{16}=\frac{1}{4}.$

⦁ Xét biến cố B: “Tích hai số ghi trên hai tấm thẻ là 1 hoặc một số nguyên tố”.

Có 6 kết quả thuận lợi cho biến cố B là: (1, 1); (1, 2); (1, 3); (1, 5); (2, 1); (3, 1). Do đó $P\left(F\right)=\frac{6}{16}=\frac{3}{8}.$

Lời giải bài tập Toán 9 Bài 26: Xác suất của biến cố liên quan tới phép thử hay khác:

• Giải Toán 9 trang 60