Giải Toán 9 trang 79 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 79 Tập 2 trong Luyện tập chung Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 79.

Giải Toán 9 trang 79 Tập 2 Kết nối tri thức

Bài 9.13 trang 79 Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng $\widehat{BOC}=120°$và $\widehat{OCA}=20°.$ Tính số đo các góc của tam giác ABC.

Lời giải:

Vì tam giác ABC nội tiếp đường tròn (O) nên OA = OB = OC.

Xét ∆OAC có OA = OC nên ∆OAC cân tại O, suy ra $\widehat{OAC}=\widehat{OCA}=20°.$

Lại có $\widehat{OAC}+\widehat{OCA}+\widehat{AOC}=180°$ (tổng các góc của một tam giác)

Suy ra $\widehat{AOC}=180°-\widehat{OAC}-\widehat{OCA}=180°-20°-20°=140°.$

Xét đường tròn (O) có:

⦁ $\widehat{ABC},\widehat{AOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AC nên:

$\widehat{ABC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2}\cdot 140°=70°.$

⦁ $\widehat{BAC},\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC nên:

$\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}\cdot 120°=60°.$

Xét ∆ABC có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng các góc của một tam giác)

Suy ra $\widehat{ACB}=180°-\widehat{BAC}-\widehat{ABC}=180°-60°-70°=50°.$

Vậy $\widehat{BAC}=60°;\widehat{ABC}=70°;\widehat{ACB}=50°.$

Bài 9.14 trang 79 Toán 9 Tập 2: Cho ABC là tam giác đều có cạnh bằng 4 cm. Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.

Lời giải:

Vẽ đường tròn (O) ngoại tiếp tam giác đều ABC.

Vì tam giác ABC đều nên đường tròn (O) có tâm là trọng tâm của tam giác và có bán kính là $R=\frac{\sqrt{3}}{3}\cdot 4=\frac{4\sqrt{3}}{3}\text{(cm).}$

Mặt khác, ta đã biết đường tròn nội tiếp tam giác đều có tâm là trọng tâm của tam giác đó, nên trọng tâm O cũng là tâm đường tròn nội tiếp tam giác đó.

Khi đó bán kính đường tròn nội tiếp tam giác ABC là $r=\frac{\sqrt{3}}{6}\cdot 4=\frac{2\sqrt{3}}{3}\text{(cm).}$

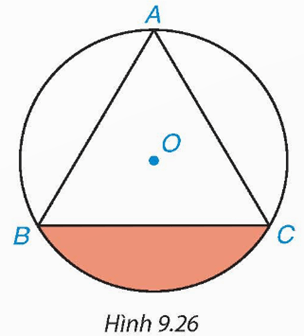
Bài 9.15 trang 79 Toán 9 Tập 2: Cho tam giác đều ABC có cạnh bằng 3 cm và nội tiếp đường tròn (O) như Hình 9.26.

a) Tính bán kính R của đường tròn (O).

b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

Lời giải:

a) Đường tròn (O) ngoại tiếp tam giác đều ABC nên có bán kính là $R=\frac{\sqrt{3}}{3}\cdot 3=\sqrt{3}\text{(cm).}$

b)

Do ∆ABC là tam giác đều nên $\widehat{BAC}=\widehat{ABC}=60°.$

Xét đường tròn (O) có $\widehat{BAC},\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC nên $\widehat{BAC}=\frac{1}{2}\widehat{BOC},$ suy ra $\widehat{BOC}=2\widehat{BAC}=2\cdot 60°=120°.$

Do đó cung nhỏ BC có số đo bằng 120°.

Diện tích hình quạt tròn bán kính $R=\sqrt{3}\text{cm}$ ứng với cung nhỏ BC có số đo bằng 120° là:

$S_q=\frac{n\pi R^2}{360}=\frac{120\cdot \pi \cdot {\left(\sqrt{3}\right)}^2}{360}=\pi {\text{(cm}}^2\text{).}$

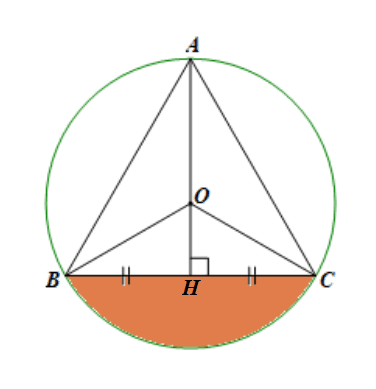
Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa là đường phân giác, cũng là đường cao của tam giác.

Vì BO là phân giác của góc ABC nên $\widehat{OBH}=\frac{1}{2}\widehat{ABC}=\frac{1}{2}\cdot 60°=30°.$

Xét ∆OBH vuông tại H, có:

$OH=OB\cdot \sin \widehat{OBH}=R\cdot \sin 30°=\frac{\sqrt{3}}{2}\text{(cm).}$

Diện tích của tam giác OBC là:

$S_{OBC}=\frac{1}{2}OH\cdot BC=\frac{1}{2}\cdot \frac{\sqrt{3}}{2}\cdot 3=\frac{3\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Gọi S là diện tích viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

Ta có: $S=S_{OBC}-S_q=\pi -\frac{3\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Vậy hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC có diện tích bằng $\pi -\frac{3\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Bài 9.16 trang 79 Toán 9 Tập 2: Trong một khu vui chơi có dạng hình tam giác đều với cạnh bằng 60 m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa là 50 m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?

Lời giải:

Gọi O là vị trí đặt cục phát wifi; ba điểm A, B, C là ba đỉnh của khu vui chơi có dạng hình tam giác đều cạnh bằng 60 m. Khi đó AB = BC = CA = 60 m.

Để vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng thì O là tâm đường tròn ngoại tiếp tam giác ABC.

Do đó bán kính đường tròn ngoại tiếp tam giác ABC là $R=\frac{\sqrt{3}}{3}\cdot 60=20\sqrt{3}\approx 34,64\text{(m).}$

Ta thấy R < 50 (m) nên bộ phát sóng đặt ở O là tâm đường tròn ngoại tiếp tam giác ABC thì cả khu vui chơi đó đều có thể bắt được sóng.

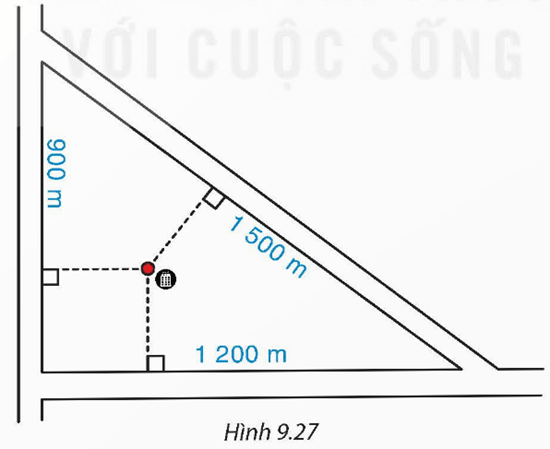
Bài 9.17 trang 79 Toán 9 Tập 2: Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900 m, 1 200 m và 1 500 m (H.9.27).

a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.

b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường

đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?

Lời giải:

Gọi A, B, C là ba đỉnh của khu dân cư sao cho AB = 900 m, BC = 1 500 m và AC = 1 200 m.

Xét ∆ABC có:

⦁ AB² + AC² = 900² + 1 200² = 2 250 000;

⦁ BC² = 1 500² = 2 250 000.

Do đó AB² + AC² = BC², nên theo định lí Pythagore đảo ta có ∆ABC vuông tại A.

a) Chu vi của phần đất giới hạn bởi tam giác ABC là:

AB + BC + CA = 900 + 1 500 + 1 200 = 3 600 (m).

Diện tích của phần đất giới hạn bởi tam giác trên là:

$S_{ABC}=\frac{1}{2}\cdot AB\cdot AC=\frac{1}{2}\cdot 900\cdot 1200=540000{\text{(m}}^2\text{).}$

b) Gọi O là vị trí xây dựng khách sạn; H, I, K lần lượt là chân đường vuông góc kẻ từ O đến AB, BC, CA.

Vì vị trí xây dựng khách sạn cách đều cả ba con đường nên OH = OI = OK.

Mặt khác, $S_{OAB}=\frac{1}{2}\cdot OH\cdot AB;$ $S_{OBC}=\frac{1}{2}\cdot OI\cdot BC;$ $S_{OCA}=\frac{1}{2}\cdot OK\cdot CA.$

Mà $S_{ABC}=S_{OAB}+S_{OBC}+S_{OCA}$

Suy ra $S_{ABC}=\frac{1}{2}\cdot OH\cdot AB+\frac{1}{2}\cdot OI\cdot BC+\frac{1}{2}\cdot OK\cdot CA$

Do đó $S_{ABC}=\frac{1}{2}\cdot OH\cdot \left(AB+BC+CA\right)$

Nên $OH=\frac{2S_{ABC}}{AB+BC+CA}=\frac{2\cdot 540000}{3600}=300\text{(m).}$

Vậy khách sạn sẽ cách mỗi con đường một khoảng là 300 mét.