Giải Toán 9 trang 8 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 8 Tập 2 trong Bài 18: Hàm số y = ax^2 (a khác 0) Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 8.
Giải Toán 9 trang 8 Tập 2 Kết nối tri thức
Luyện tập 2 trang 8 Toán 9 Tập 2: Vẽ đồ thị của hàm số Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
Lời giải:
Lập bảng một số giá trị tương ứng giữa x và y:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
2 |
0,5 |
0 |
0,5 |
2 |
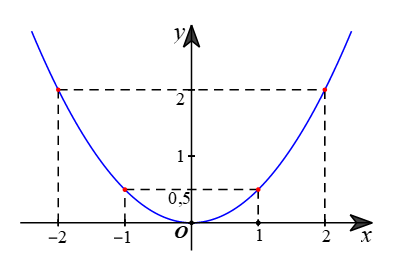
Biểu diễn các điểm (–2; 2); (–1; 0,5); (0; 0); (1; 0,5) và (2; 2) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số như hình vẽ dưới đây:
Ta có y = 2 nên hay x2 = 4. Suy ra x = 2 hoặc x = –2.
Vậy ta có hai điểm cần tìm là (–2; 2) và (2; 2). Hai điểm này đối xứng với nhau qua trục tung Oy.
Vận dụng 2 trang 8 Toán 9 Tập 2: Giải quyết bài toán ở tình huống mở đầu.
Lời giải:
Vì các dây cáp có dạng đồ thị của hàm số y = ax2 (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax2 (a ≠ 0) đi qua điểm B(200; 75).
Thay x = 200 và y = 75 vào hàm số y = ax2, ta được:
75 = a . 2002, hay 40 000a = 75, suy ra a = 0,001875 (thỏa mãn a ≠ 0).
Khi đó ta có hàm số y = 0,001875x2.
Chiều cao CH của dây cáp chính là tung độ của điểm C thuộc đồ thị hàm số y = 0,001875x2.
Thay hoành độ điểm C là x = 100 vào hàm số y = 0,001875x2, ta được:
y = 0,001875 . 1002 = 18,75.
Vậy chiều cao CH của dây cáp là 18,75 mét.
Bài 6.1 trang 8 Toán 9 Tập 2: Cho hàm số y = 0,25x2. Hoàn thành bảng giá trị sau vào vở:
Lời giải:
Thay lần lượt các giá trị x = –3; x = –2; …; x = 3 vào hàm số y = 0,25x2, ta được bảng giá trị:
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
y |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
Bài 6.2 trang 8 Toán 9 Tập 2: Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.
a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Lời giải:
a) Thể tích của hình lăng trụ đứng đó là: V = Bh = 10a2 (cm3).
Vậy công thức tính thể tích V của lăng trụ là V = 10a2 (cm3).
Khi a = 2 cm, thay vào công thức V = 10a2, ta được:
V = 10 . 22 = 40 (cm3).
Vậy V = 40 cm3 khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì độ dài cạnh đáy lúc này là 2a (cm).
Thể tích của hình lăng trụ lúc này là:
V’ = B’.h = 10 . (2a)2 = 40a2 = 4V (cm3).
Vậy nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ tăng lên 4 lần.
Bài 6.3 trang 8 Toán 9 Tập 2: Diện tích toàn phần S (cm2) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm2.
Lời giải:
a) Diện tích toàn phần của hình lập phương là:
S = 2 . a2 + 4 . a2 = 6a2 (cm2).
Vậy công thức của hàm số cần tìm là: S = 6a2 (cm2).
b) Ta có S = 54 cm2, thay vào công thức S = 6a2, ta được:
54 = 6a2, hay a2 = 9. Suy ra a = 3 (do a > 0).
Vậy một hình lập phương có diện tích toàn phần là 54 cm2 thì có độ dài cạnh bằng 3 cm.
Bài 6.4 trang 8 Toán 9 Tập 2: Vẽ đồ thị của các hàm số sau:
a) y = 3x2.
b)
Lời giải:
a) Lập bảng một số giá trị tương ứng giữa x và y:
x |
–1 |
–0,5 |
0 |
0,5 |
1 |
y = 3x2 |
3 |
0,75 |
0 |
0,75 |
3 |
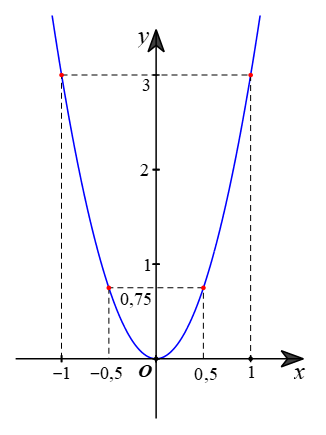
Biểu diễn các điểm (–1; 3); (–0,5; 0,75); (0; 0); (0,5; 0,75) và (1; 3) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số y = 3x2 như hình vẽ dưới đây:
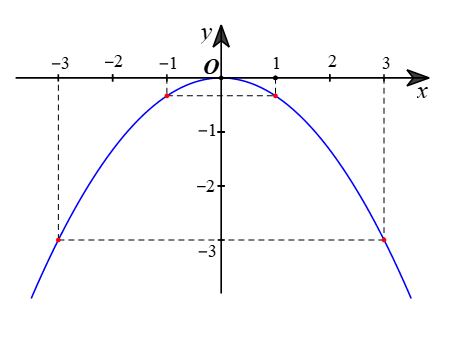
b) Lập bảng một số giá trị tương ứng giữa x và y:
x |
–3 |
–1 |
0 |
1 |
3 |
–3 |
0 |
–3 |
Biểu diễn các điểm (–2; 2); (–1; 0,5); (0; 0); (1; 0,5) và (2; 2) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số như hình vẽ dưới đây:
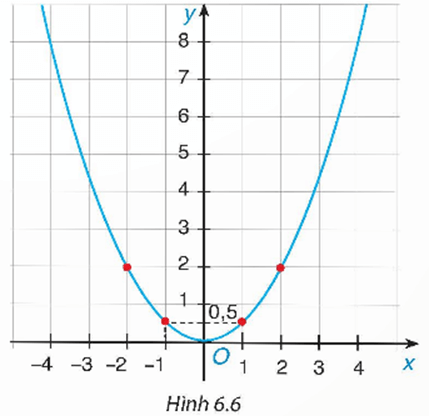
Bài 6.5 trang 8 Toán 9 Tập 2: Biết rằng đường cong trong Hình 6.6 là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –2.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
Lời giải:
a) Do parabol y = ax2 trong Hình 6.6 đi qua điểm có tọa độ (2; 2) nên ta thay x = 2 và y = 2 vào hàm số y = ax2 thì được:
2 = a . 22, hay 4a = 2. Suy ra a = .
b) Trên Hình 6.6, ta thấy parabol đi qua điểm có tọa độ (–2; 2).
Vậy điểm thuộc parabol có hoành độ x = –2 thì có tung độ là 2.
c) Với a = ta có hàm số
Thay y = 8 vào hàm số trên, ta được: hay x2 = 16.
Suy ra x = 4 hoặc x = –4.
Vậy các điểm thuộc parabol cần tìm là (–4; 8) và (4; 8).
Lời giải bài tập Toán 9 Bài 18: Hàm số y = ax^2 (a khác 0) hay khác: