Giải Toán 9 trang 92 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 92 Tập 2 trong Bài tập cuối chương 9 Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 92.

Giải Toán 9 trang 92 Tập 2 Kết nối tri thức

Bài 9.37 trang 92 Toán 9 Tập 2: Khẳng định nào sau đây là đúng?

A. Góc nội tiếp có số đo bằng số đo cung bị chắn.

B. Góc có hai cạnh chứa các dây cung của đường tròn là góc nội tiếp đường tròn đó.

C. Góc nội tiếp có số đo bằng một nửa số đo cung bị chắn.

D. Góc có đỉnh nằm trên đường tròn là góc nội tiếp đường tròn đó.

Lời giải:

Đáp án đúng là: C

Trong một đường tròn hoặc hai đường tròn bằng nhau:

⦁ Góc nội tiếp có số đo bằng nửa số đo cung bị chắn. Do đó phương án A là sai và phương án C là đúng.

⦁ Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó nên phương án B và D là sai.

Vậy ta chọn phương án C.

Bài 9.38 trang 92 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp một đường tròn có $\hat{A}-\hat{C}=100°.$ Khẳng định nào dưới đây là đúng?

A. $\hat{A}=80°.$

B. $\hat{C}=80°.$

C. $\hat{B}+\hat{D}=100°.$

D. $\hat{A}=140°.$

Lời giải:

Đáp án đúng là: D

Vì tứ giác ABCD nội tiếp một đường tròn nên tổng hai góc đối nhau bằng 180°, do đó $\hat{B}+\hat{D}=180°;$ $\hat{A}+\hat{C}=180°.$

Mà $\hat{A}-\hat{C}=100°$ nên $\hat{A}=\frac{180°+100°}{2}=140°$ và $\hat{C}=\frac{180°-100°}{2}=40°.$

Bài 9.39 trang 92 Toán 9 Tập 2: Đa giác nào dưới đây không nội tiếp một đường tròn?

A. Đa giác đều.

B. Hình chữ nhật.

C. Hình bình hành.

D. Tam giác.

Lời giải:

Đáp án đúng là: C

Các tam giác, hình chữ nhật, đa giác đều là các đa giác nội tiếp được một đường tròn.

Hình bình hành không là đa giác nội tiếp đường tròn.

Vậy ta chọn phương án C.

Bài 9.40 trang 92 Toán 9 Tập 2: Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:

a) Tứ giác AEHF nội tiếp đường tròn tâm I;

b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.

Lời giải:

a) Vì tam giác ABC có các đường cao BE, CF cắt nhau tại H nên HE ⊥ AE và HF ⊥ AF.

Vì ∆AEH vuông tại E nên đường tròn ngoại tiếp của tam giác có tâm I, đường kính AH. Do đó ba điểm A, E, H cùng nằm trên đường tròn tâm I, đường kính AH.

Vì ∆AFH vuông tại F nên đường tròn ngoại tiếp của tam giác có tâm I, đường kính AH. Do đó ba điểm A, F, H cùng nằm trên đường tròn tâm I, đường kính AH.

Suy ra bốn điểm A, E, H, F cùng nằm trên đường tròn tâm I, đường kính AH.

Vậy tứ giác AEHF là tứ giác nội tiếp đường tròn tâm I, đường kính AH.

b)

Xét ∆IAF có IA = IF (do A, F thuộc đường tròn tâm I đường kính AH) nên ∆IAF cân tại I, suy ra $\widehat{IAF}=\widehat{IFA}.\left(1\right)$

Xét ∆BCF vuông tại F có FM là trung tuyến ứng với cạnh huyền BC nên FM = MB = MC = $\frac{1}{2}$BC.

Xét ∆BMF có MB = MF nên ∆BMF cân tại M, suy ra $\widehat{MFB}=\widehat{MBF}.\left(2\right)$

Kéo dài AH cắt BC tại D, khi đó AD là đường cao của tam giác ABC.

Xét ∆ABD vuông tại D, ta có:

$\widehat{BAD}+\widehat{ABD}=90°$ (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Do đó $\widehat{IFA}+\widehat{MFB}=\widehat{IAF}+\widehat{MBF}=\widehat{BAD}+\widehat{ABD}=90°.$

Lại có $\widehat{IFA}+\widehat{IFM}+\widehat{MFB}=180°$

Suy ra $\widehat{IFM}=180°-\left(\widehat{IFA}+\widehat{MFB}\right)=180°-90°=90°.$

Hay MF ⊥ IF, mà IF là bán kính đường tròn ngoại tiếp tứ giác AEHF.

Do đó MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.

Tương tự, ta cũng chứng minh được ME tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.

Vậy ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.

Bài 9.41 trang 92 Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.

Lời giải:

Vì tam giác ABC nội tiếp đường tròn (O).

Mà M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB nên OM, ON, OP là ba đường trung trực của tam giác ABC.

Do đó OM ⊥ BC, ON ⊥ CA, OP ⊥ AB.

Vì ∆OAN vuông tại N nên tam giác nội tiếp đường tròn có đường kính OA. Do đó O, A, N nằm trên đường tròn đường kính OA.

Vì ∆OAP vuông tại P nên tam giác nội tiếp đường tròn đường kính OA. Do đó O, A, P nằm trên đường tròn đường kính OA.

Suy ra bốn điểm A, N, O, P nằm trên đường tròn đường kính OA.

Vì vậy, tứ giác ANOP nội tiếp đường tròn đường kính OA.

Chứng minh tương tự, ta có BPOM nội tiếp đường tròn đường kính OB, CMON nội tiếp đường tròn đường kính OC.

Vậy ANOP, BPOM, CMON là các tứ giác nội tiếp.

Bài 9.42 trang 92 Toán 9 Tập 2: Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3 cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.

Lời giải:

Giả sử ABCDEG là hình lục giác đều và MNPQ là hình vuông cùng nội tiếp đường tròn (O; R). Do đó OA = OB = OC = OD = OE = OM = ON = OP = OQ = R.

Vì MNPQ là hình vuông nên đường tròn ngoại tiếp hình vuông này có tâm là giao điểm hai đường chéo.

Mặt khác, hai đường chéo MP, NQ vuông góc với nhau tại trung điểm O của mỗi đường.

Xét ∆OMN vuông tại O, theo định lí Pythagore ta có:

MN² = OM² + ON²

Suy ra 3² = R² + R², hay 2R² = 9 nên $R=\sqrt{\frac{9}{2}}=\frac{3\sqrt{2}}{2}\text{(cm).}$

Vì ABCDEG nên AB = BC = CD = DE = EG = GA.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC.

Do đó ∆OAB = ∆OBC (c.c.c).

Chứng minh tương tự ta có

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOA.

Suy ra $\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOG}=\widehat{GOA}.$

Mà $\widehat{AOB}+\widehat{BOC}+\widehat{COD}+\widehat{DOE}+\widehat{EOG}+\widehat{GOA}=360°$

Do đó $6\widehat{AOB}=360°$

Suy ra $\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOG}=\widehat{GOA}=\frac{360°}{6}=60°.$

Xét ∆OAB có OA = OB và $\widehat{AOB}=60°$ nên là tam giác đều.

Như vậy các tam giác BOC, COD, DOE, EOG, GOA cũng đều là tam giác đều.

Do đó AB = BC = CD = DE = EG = GA = OA = R = $\frac{3\sqrt{2}}{2}$ (cm).

Khi đó chu vi của hình lục giác đều ABCDEG là:

AB + BC + CD + DE + EG + GA = 6R = $6\cdot \frac{3\sqrt{2}}{2}=9\sqrt{2}\text{(cm).}$

⦁ Gọi H là trung điểm của AB.

Tam giác ABC đều có OH là đường trung tuyến nên cũng là đường cao của tam giác.

Xét ∆OAH vuông tại H, ta có:

OH = OA.sin$\widehat{OAH}=\frac{3\sqrt{2}}{2}\cdot \sin 60°=\frac{3\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}=\frac{3\sqrt{6}}{4}\text{(cm).}$

Diện tích của tam giác đều OAB là:

$S_{OAB}=\frac{1}{2}\cdot OH\cdot AB=\frac{1}{2}\cdot \frac{3\sqrt{6}}{4}\cdot \frac{3\sqrt{2}}{2}=\frac{9\sqrt{3}}{8}{\text{(cm}}^2\text{).}$

Diện tích của hình lục giác đều là: $S=6S_{OAB}=6\cdot \frac{9\sqrt{3}}{8}=\frac{27\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Bài 9.43 trang 92 Toán 9 Tập 2:

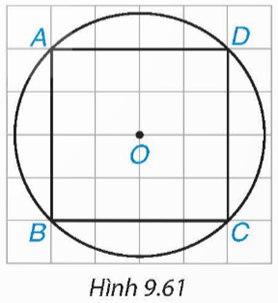
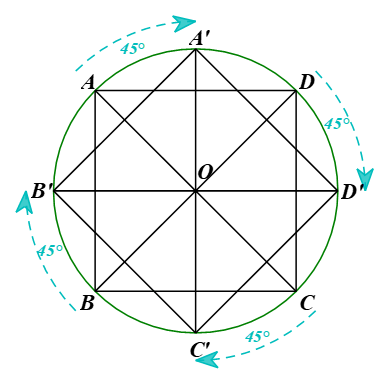
a) Phép quay thuận chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’.

b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?

Lời giải:

a)

⦁ Lấy điểm A’ thuộc đường tròn (O) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ và $\widehat{AO{A}^{\text{'}}}=45°.$

⦁ Xác định các điểm B’, C’, D’ tương tự như cách xác định điểm A’ ở trên. Nối A’ với B’, B’ với C’, C’ với D’. Khi đó ta được tứ giác A’B’C’D’.

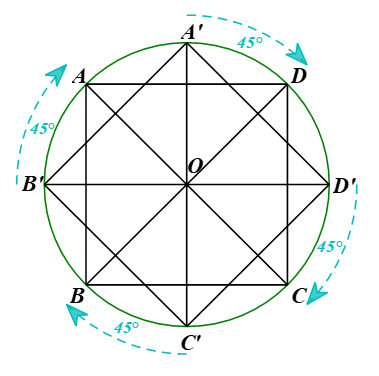
b)

Vì ABCD là hình vuông nên đường tròn ngoại tiếp hình vuông này có tâm là giao điểm hai đường chéo.

Mặt khác, hai đường chéo AC, BD vuông góc với nhau tại trung điểm O của mỗi đường.

Ta có: $\widehat{AOD}=\widehat{AO{A}^{\text{'}}}+\widehat{A^{\text{'}}OD}$ nên $90°=45°+\widehat{A^{\text{'}}OD},$ suy ra $\widehat{A^{\text{'}}OD}=90°-45°=45°.$

Do đó phép quay thuận chiều 45° tâm O biến điểm A’ thành điểm D.

Tương tự, phép quay thuận chiều 45° tâm O biến các điểm B’, C’, D’ lần lượt thành các điểm A, B, C.

Vậy phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm D, A, B, C.

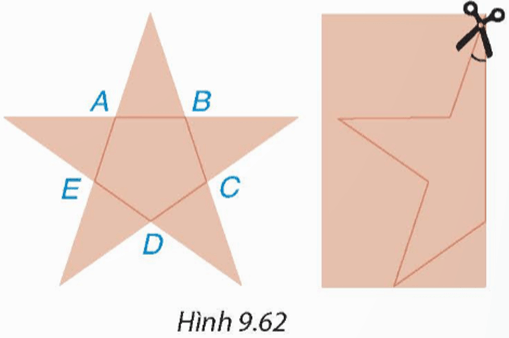
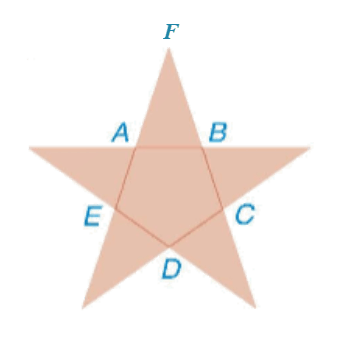
Bài 9.44 trang 92 Toán 9 Tập 2: Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Hỏi góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu độ?

Lời giải:

Ngũ giác đều ABCDE được tạo bởi ba tam giác là ABC, ACD và ADE. Mà mỗi tam giác có tổng các góc bằng 180° nên tổng số đo 5 góc của ngũ giác đều ABCDE là: 3.180° = 540°.

Vì ABCDE là ngũ giác đều nên các góc của ngũ giác bằng nhau và bằng $\frac{540°}{5}=108°.$

Gọi F là đỉnh của tam giác cân có cạnh đáy là AB (hình vẽ).

Ta có: $\widehat{FAB}+\widehat{BAE}=180°$ (hai góc kề bù)

Suy ra $\widehat{FAB}=180°-\widehat{BAE}=180°–108°=72°.$

Tam giác FAB cân tại F nên $\widehat{FAB}=\widehat{FBA}=72°.$

Mặt khác, $\widehat{AFB}+\widehat{FAB}+\widehat{FBA}=180°$ (tổng ba góc của một tam giác)

Nên $\widehat{AFB}=180°-\widehat{FAB}-\widehat{FBA}=180°-72°-72°=36°.$

Vậy góc tạo bởi lưỡi kéo và nếp gấp lúc đầu là $\frac{1}{2}\widehat{AFB}=\frac{1}{2}\cdot 36°=18°.$