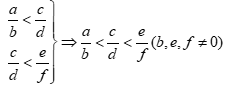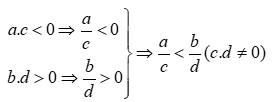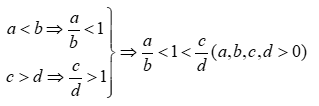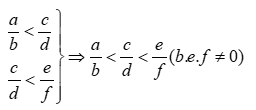Chuyên đề Phân số và số thập phân lớp 6 (Cánh diều)

---

Haylamdo biên soạn và sưu tầm tài liệu chuyên đề Phân số và số thập phân Toán 6 sách Cánh diều gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 6.

Chuyên đề Phân số và số thập phân lớp 6 (Cánh diều)

Xem thử

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 6 Cánh diều bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

CHUYÊN ĐỀ 1: SO SÁNH PHÂN SỐ

PHẦN I. TÓM TẮT LÍ THUYẾT.

1. So sánh hai phân số cùng mẫu.

- Trong hai phân số cùng mẫu dương:

+ Phân số nào có tử số lớn hơn thì lớn hơn.

+ Phân số nào có tử số bé hơn thì bé hơn.

+ Nếu tử số của hai phân số bằng nhau thì hai phân số đó bằng nhau.

2. So sánh hai phân số khác mẫu

Muốn so sánh hai phân số khác mẫu ta quy đồng mẫu hai phân số đó, rồi thực hiện so sánh hai phân số cùng mẫu.

Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy đồng.

3. Trong hai phân số có cùng tử số

- Trong hai phân số cùng tử số dương:

+ Phân số nào có mẫu số lớn hơn thì bé hơn.

+ Phân số nào có mẫu số bé hơn thì lớn hơn.

+ Nếu mẫu số của hai phân số bằng nhau thì hai phân số đó bằng nhau.

4. Các tính chất

+ Phân số có tử và mẫu cùng dấu là phân số dương. Mọi phân số dương đều lớn hơn 0.

+ Phân số có tử và mẫu trái dấu là phân số âm. Mọi phân số âm đều nhỏ hơn 0.

+ Nếu cộng cả tử và mẫu của một phân số nhỏ hơn 1, tử và mẫu đều dương, với cùng một số nguyên dương thì giá trị của phân số đó tăng thêm $\frac{a}{b}<\frac{a+c}{b+c}(a,b,c>0).$

+ Với hai phân số có cả tử $\frac{a}{b}$ và $\frac{c}{d}$ mẫu dương và thì $\frac{a}{b}<\frac{c}{d}\Rightarrow \frac{a}{b}<\frac{a+c}{b+d}(a,b,c,d>0)$

+ Tính chất bắc cầu:

+ Với mọi m$\ne$0:

$*\frac{a}{b}<1\Rightarrow \frac{a}{b}<\frac{a+m}{b+m}$

$*\frac{a}{b}=1\Rightarrow \frac{a}{b}=\frac{a+m}{b+m}.$

$*\frac{a}{b}>1\Rightarrow \frac{a}{b}>\frac{a+m}{b+m}$

$*\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}.$

PHẦN II. CÁC DẠNG BÀI.

I. Phương pháp giải.

- Trong hai phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn: $a<c\iff \frac{a}{b}<\frac{c}{b}\left(b>0\right)$

II. Bài toán.

Lời giải

a) Ta có: $3>1$ và $4>0$ nên $\frac{3}{4}>\frac{1}{4}$.

b) Ta có: $-3\text{>}-4$ và $5>0$ nên $\frac{-3}{5}>\frac{-4}{5}$.

c) Ta có: $6>5$ và $7>0$ nên $\frac{5}{7}<\frac{6}{7}$.

d) Ta có: $25>15$ và $27>0$ nên $\frac{15}{37}<\frac{25}{37}$.

Lời giải

Các phân số ở bài này chưa có mẫu dương, trước hết ta sẽ đưa chúng về các phân số có mẫu dương trước khi so sánh.

a) Vì $\frac{1}{-4}=\frac{-1}{4}$;

Ta có: $-3<-1$ và $4>0$ nên $\frac{-3}{4}<\frac{-1}{4}\Rightarrow \frac{-3}{4}<\frac{1}{-4}$.

b) Vì $\frac{7}{-8}=\frac{-7}{8}$;

Ta có: $-7<-3$ và $8>0$ nên $\frac{-7}{8}<\frac{-3}{8}\Rightarrow \frac{7}{-8}<\frac{-3}{8}$.

c) Vì $\frac{-7}{-17}=\frac{7}{17}$;

Ta có: $6\text{<}7$ và $17>0$ nên $\frac{6}{17}<\frac{7}{17}\Rightarrow \frac{6}{17}<\frac{-7}{-17}$.

d) Vì $\frac{25}{-47}=\frac{-25}{47}$;

Ta có: $-25<-17$ và $47>0$ nên $\frac{-25}{47}<\frac{-17}{47}\Rightarrow \frac{25}{-47}<\frac{-17}{45}$.

Lời giải

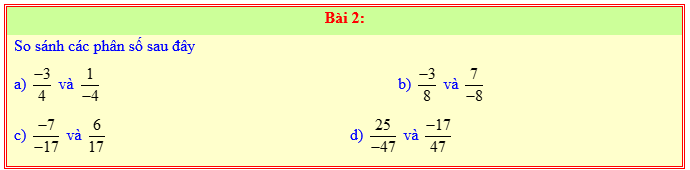
Nhận xét: Các phân số trong bài có cùng mẫu số dương, nên để sắp xếp các phân số theo thứ tự tăng dần ta so sánh các tử số.

a) $\frac{-5}{17};\frac{5}{17};\frac{2}{17};\frac{-4}{17};\frac{0}{17};\frac{-11}{17};\frac{7}{17}$

Ta có: -11 < -5 < -4 <0 < 2 < 5< 7 và 17 > 0

nên $\frac{-11}{17}<\frac{-5}{17}<\frac{-4}{17}<\frac{0}{17}<\frac{2}{17}<\frac{5}{17}<\frac{7}{17}$.

b) $\frac{-15}{57};\frac{5}{57};\frac{12}{57};\frac{14}{57};\frac{10}{57};\frac{-14}{57};\frac{27}{57}$

Ta có: -15 < -14 < 5 < 10 < 12 <14 < 27 và 57 > 0

nên $\frac{-15}{57}<\frac{-14}{57}<\frac{5}{57}<\frac{10}{57}<\frac{12}{57}<\frac{14}{57}<\frac{27}{57}$

c) $\frac{-15}{37};\frac{-16}{37};\frac{32}{37};\frac{13}{37};\frac{10}{37};\frac{-18}{37};\frac{23}{37}$

Ta có: -18 < -16 < -15 < 10 < 13 < 23 < 32 và 37 > 0

Nên $\frac{-18}{37}<\frac{-16}{37}<\frac{-15}{37}<\frac{10}{37}<\frac{13}{37}<\frac{23}{37}<\frac{32}{37}$.

Lời giải

a) $\frac{10}{15}<\frac{11}{15}<\frac{12}{15}<\frac{13}{15}<\frac{14}{15}<\frac{15}{15}$.

b) $\frac{-11}{17}<\frac{-10}{17}<\frac{-9}{17}<\frac{-8}{17}<\frac{-7}{17}<\frac{-6}{17}$.

c) $\frac{-8}{37}<\frac{7}{-37}<\frac{-6}{37}<\frac{5}{-37}<\frac{-4}{37}.$

I. Phương pháp giải.

Cách 1. Quy đồng mẫu số hai phân số rồi so sánh các tử số của chúng.

- Bước 1: Quy đồng mẫu số của hai phân số (đưa các phân số về cùng mẫu số)

- Bước 2: So sánh tử số của hai phân số cùng mẫu số đã quy đồng.

Trong hai phân số có cùng mẫu số:

+ Phân số nào có tử số nhỏ hơn thì nhỏ hơn.

+Phân số nào có tử số lớn hơn thì lớn hơn.

Cách 2. Quy đồng tử số hai phân số rồi so sánh các mẫu số của chúng.

- Bước 1: Quy đồng tử số (đưa về cùng tử số)

+ Lấy tử số và mẫu số của phân số thứ nhất nhân tử số của phân số thứ hai.

+ Lấy tử số và mẫu số của phân số thứ hai nhân tử số của phân số thứ nhất.
- Bước 2: So sánh mẫu số của hai phân số đã quy đồng tử số.

Trong hai phân số có cùng tử số:

+ Phân số nào có mẫu số nhỏ hơn thì lớn hơn

+Phân số nào có mẫu số lớn hơn thì nhỏ hơn.

Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy đồng.

II. Bài toán.

Lời giải

Cách 1: Quy đồng mẫu số 2PS rồi so sánh tử số của chúng với nhau.

+ Ta có: mẫu chung là 35

+ So sánh 2PS đã quy đồng, ta có: $\frac{14}{35}<\frac{20}{35}$ (vì 2 PS có cùng mẫu số, tử số có $14<20$) nên $\frac{2}{5}<\frac{4}{7}$.

Cách 2: Chọn tử số chung là 4 (vì $4:2=2$)

Ta có: $\frac{2}{5}=\frac{2\times 2}{5\times 2}=\frac{4}{10};$ giữ nguyên $\frac{4}{7}$

Ta có $:\frac{4}{10}<\frac{4}{7}(\text{TS}=4$, mẫu số có $10>7$) nên $\frac{2}{5}<\frac{4}{7}$.

Lời giải

Có MC: 4.5 = 20

$\frac{-3}{4}=\frac{(-3).5}{4.5}=\frac{-15}{20}$;

$\frac{-4}{5}=\frac{(-4).4}{5.4}=\frac{-16}{20}$

Vì: - 15 > - 16 nên $\frac{-15}{20}>\frac{-16}{20}$ hay: $\frac{-3}{4}>\frac{-4}{5}$. Vậy: $\frac{-3}{4}>\frac{-4}{5}$

Lời giải

a) $\frac{-11}{12}$ và $\frac{17}{-18}\Rightarrow \frac{-11}{12}$ và $\frac{-17}{18}$

Có: MC: 2².3² = 36

$\frac{-11}{12}=\frac{(-11).3}{12.3}=\frac{-33}{36}$

$\frac{-17}{18}=\frac{(-17).2}{18.2}=\frac{-34}{36}$

Vì $\frac{-33}{36}>\frac{-34}{36}$ nên $\frac{-11}{12}>\frac{-17}{18}$

Vậy: $\frac{-11}{12}>\frac{17}{-18}$

b) $\frac{-14}{21}$ và $\frac{-60}{-72}$ $\Rightarrow \frac{-2}{3}$ và $\frac{5}{6}$

Có MC: 6

$\frac{-2}{3}=\frac{(-2).2}{3.2}=\frac{-4}{6}$

Vì $\frac{-4}{6}<\frac{5}{6}$ nên $\frac{-2}{3}<\frac{5}{6}$

Vậy: $\frac{-14}{21}<\frac{-60}{-72}$

Lời giải

a) $\frac{2}{3}h$ và $\frac{3}{4}h$

Có MC: 12

$\frac{2}{3}=\frac{2.4}{3.4}=\frac{8}{12};\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$

Vì $\frac{9}{12}>\frac{8}{12}$ nên $\frac{3}{4}h$ dài hơn $\frac{2}{3}h$

b) $\frac{7}{10}m$ và $\frac{3}{4}m$

Có MC: $2^2.5=20$

$\frac{7}{10}=\frac{7.2}{10.2}=\frac{14}{20};\frac{3}{4}=\frac{3.5}{4.5}=\frac{15}{20}$

Vì $\frac{14}{20}<\frac{15}{20}$ nên $\frac{7}{10}m$ngắn hơn $\frac{3}{4}m$

c)

Ta có: $\frac{9}{10}>\frac{7}{10}$ (vì 9>7)

nên $\frac{9}{10}kg$ lớn hơn $\frac{7}{10}kg$

d)

Ta có: $\frac{7}{9}=\frac{42}{54};\frac{5}{6}=\frac{45}{54}$

mà $42<45\Rightarrow \frac{42}{54}<\frac{45}{54}$

Vậy $\frac{7}{9}km/h$ nhỏ hơn $\frac{5}{6}km/h$

Lời giải

Cách 1: QĐMS (chọn MSC = 12)

Ta có:

$\frac{2}{3}=\frac{2\times 4}{3\times 4}=\frac{8}{12};\frac{3}{4}=\frac{3\times 3}{4\times 3}=\frac{9}{12}$

Vì $\frac{8}{12}<\frac{9}{12}$ nên $\frac{2}{3}<\frac{3}{4}$

Cách 2: QĐTS (chọn TSC = 6)

Ta có:

$\frac{2}{3}=\frac{2\times 3}{3\times 3}=\frac{6}{9};\frac{3}{4}=\frac{3\times 2}{4\times 2}=\frac{6}{8}$

Vì $\frac{6}{9}<\frac{6}{8}$ nên $\frac{2}{3}<\frac{3}{4}$

Lời giải

Để sắp xếp các PS theo thứ tự từ bé đến lớn, trước tiên ta QĐMS các PS này. Rồi so sánh tử số.

a)

Chọn $\text{MSC}=18$(vì 18 chia hết cho 6; 9; 18)

$\frac{8}{9}=\frac{8\times 2}{9\times 2}=\frac{16}{18};\frac{5}{6}=\frac{5\times 3}{6\times 3}=\frac{15}{18};$ giữ nguyên$\frac{17}{18}$

Ta so sánh các PS đã quy đồng mẫu số:

Vì $\frac{15}{18}<\frac{16}{18}<\frac{17}{18}$ nên $\frac{5}{6}<\frac{8}{9}<\frac{17}{18}$

Vậy các phân số được viết theo thứ tự từ bé đến lớn là: $\frac{5}{6};\frac{8}{9};\frac{17}{18}$

b)

Chọn MSC = 8 (vì 8 chia hết cho 2 ; 4; 8)

Ta có: Vì $\frac{1}{2}=\frac{4}{8};\frac{3}{4}=\frac{6}{8}$nên $\frac{1}{2}<\frac{5}{8}<\frac{3}{4}$, giữ nguyên $\frac{5}{8}$

Vì $\frac{4}{8}<\frac{5}{8}<\frac{6}{8}$ nên $\frac{1}{2}<\frac{5}{8}<\frac{3}{4}$

Vậy các phân số được viết theo thứ tự từ bé đến lớn là: $\frac{1}{2};\frac{5}{8};\frac{3}{4}$

Lời giải

Do các số âm luôn nhỏ hơn các số dương nên $\frac{3}{4};\frac{5}{6};-\frac{2}{9};-\frac{1}{12};-\frac{5}{8}$

Trong các số dương thì $\frac{5}{6}>\frac{3}{4}$

Vì $\frac{2}{9}<\frac{5}{12}<\frac{5}{8}$nên $-\frac{2}{9}>-\frac{5}{8}$

Vì $\frac{2}{9}>\frac{2}{12}>\frac{1}{12}$ nên $-\frac{2}{9}<-\frac{1}{12}$

Vậy chúng ta có thể sắp xếp theo yêu cầu đề bài: $\frac{5}{6};\frac{3}{4};-\frac{1}{12};-\frac{2}{9};-\frac{5}{8};$

I. Phương pháp giải.

- Khi so sánh hai hay nhiều phân số, việc quy đồng đưa về cùng một mẫu số dương để so sánh tử số nhiều khi khá khó khăn, do đó, ta có thể chọn một phân số trung gian, dựa vào phân số trung gian này, ta sẽ so sánh được hai phân số ban đầu.

* Dạng 3.1: So sánh qua số 0

- Việc so sánh qua số 0 được sử dụng khi ta thấy một phân số nhỏ hơn 0 (tử và mẫu trái dấu) và một phân số lớn hơn không (tử và mẫu cùng dấu).

* Dạng 3.2: So sánh qua số 1

- Với hai phân số cùng dương mà ta nhận thấy một phân số lớn hơn 1 ( tử số lớn hơn mẫu số) và một phân số nhỏ hơn 1 ( tử số nhỏ hơn mẫu số) thì ta sẽ chọn 1 là số trung gian để so sánh.

* Dạng 3.3: So sánh qua một phân số trung gian phù hợp

Ta cũng có thể chọn một phân số trung gian phù hợp để so sánh hai phân số

Chú ý một vài tính chất sau đây:

+ Trong hai phân số có cùng tử, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì lớn hơn

................................

................................

................................

Xem thử