Cho hình chữ nhật ABCD với O là giao điểm của hai đường chéo AC và BD
Cho hình chữ nhật ABCD với O là giao điểm của hai đường chéo AC và BD.
Giải vở thực hành Toán 6 Chân trời sáng tạo Bài 5: Trung điểm của đoạn thẳng
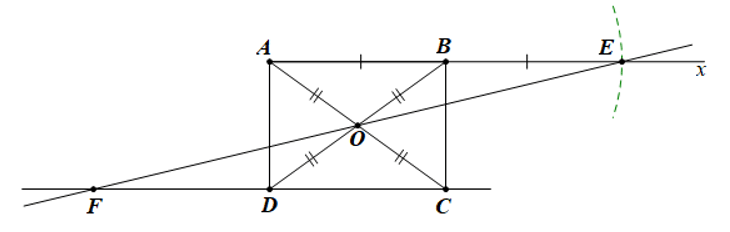
Bài 1 trang 63 vở thực hành Toán lớp 6 Tập 2: Cho hình chữ nhật ABCD với O là giao điểm của hai đường chéo AC và BD.
a) Hãy liệt kê các đoạn thẳng nhận O làm trung điểm.
b) Nêu cách vẽ điểm E sao cho B là trung điểm AE.
c) Đường thẳng EO cắt đường thẳng CD tại F. Điểm D có phải là trung điểm của CF không? Em hãy nêu cách kiểm tra dự đoán đó.
Lời giải:
a) Các đoạn thẳng nhận O làm trung điểm là AC và BD.
b) Dùng thước và compa vẽ điểm E sao cho B là trung điểm của AE.
‒ Bước 1: Vẽ tia đối Bx của tia BA;
‒ Bước 2: Vẽ điểm E:
• Cách 1: Dùng thước thẳng:
Đo độ dài đoạn thẳng AB. Trên tia Bx lấy một điểm E sao cho BE = AB.
• Cách 2: Dùng compa:
Lấy B làm tâm, vẽ đường tròn bán kính BA, cắt tia Bx tại một điểm.
Điểm này là điểm E.
Qua hai cách vẽ trên ta được điểm B là trung điểm AE.
c) Điểm D có là trung điểm của CF.
Điểm D nằm giữa hai điểm C, F và DC = DF.
Ta có thể dùng hai cách sau để kiểm tra dự đoán trên:
Cách 1: Dùng thước thẳng:
Đo độ dài đoạn thẳng DC và DF và kiểm tra xem hai đoạn thẳng này có bằng nhau hay không.
Cách 2: Dùng compa:
Lấy D làm tâm, vẽ đường tròn bán kính DC, cắt tia đối của tia DC tại một điểm, kiểm tra xem điểm này có trùng điểm F hay không.
Kết quả: D là trung điểm của CF.
Lời giải vở thực hành Toán lớp 6 Bài 5: Trung điểm của đoạn thẳng hay khác: