Giải Vở thực hành Toán 7 trang 50 Tập 2 Chân trời sáng tạo
Với Giải VTH Toán 7 trang 50 Tập 2 trong Bài 5: Đường trung trực của một đoạn thẳng Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 50.
Giải VTH Toán 7 trang 50 Tập 2 Chân trời sáng tạo
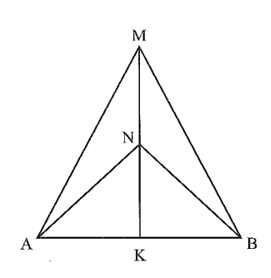
Bài 6 trang 50 Vở thực hành Toán 7 Tập 2: Hình vẽ bên dưới có tam giác MAB cân tại M, tam giác NAB cân tại N. Chứng minh MN là đường trung trực của AB.
Lời giải:
Xét tam giác MNA và tam giác MNB.
MA = MB ( do tam giác MAB cân tại M).
NA = NB ( do tam giác NAB cân tại N).
Cạnh chung MN.
Vậy tam giác MNA bằng tam giác MNB theo trường hợp c.c.c.
Suy ra .
Xét tam giác MAK và tam giác MBK.
( do ).
MA = MB ( do tam giác MAB cân tại M).
Cạnh chung MK.
Vậy tam giác MAK bằng tam giác MBK theo trường hợp c.g.c.
Suy ra KA = KB (1) và mà nên hay MK vuông góc với AB hay MN vuông góc với AB (2).
Từ (1) và (2) suy ra MN là đường trung trực của AB.
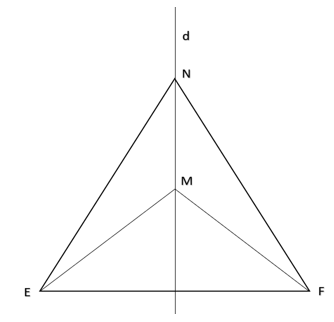
Bài 7 trang 50 Vở thực hành Toán 7 Tập 2: Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF. Chứng minh rằng ∆ EMN = ∆ FMN.
Lời giải:
Xét tam giác EMN và tam giác FMN.
ME = MF ( do M nằm trên đường trung trực của EF).
NE = NF ( do N nằm trên đường trung trực của EF).
Cạnh chung MN.
Vậy ∆ EMN = ∆ FMN theo trường hợp c.c.c.
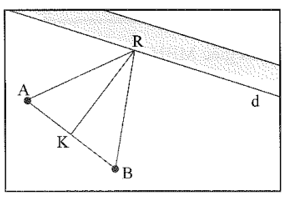
Bài 8 trang 50 Vở thực hành Toán 7 Tập 2: Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B. Hãy tìm bên đường một địa điểm M để xây dựng một trạm xe buýt sao cho trạm xe cách đều hai điểm dân cư.
Lời giải:
Vẽ đường trung trực của AB cắt con đường tại điểm R.
R là điểm nằm trên đường trung trực của AB nên RA = RB.
Vậy trạm xe buýt xây dựng tại R.
Lời giải Vở thực hành Toán 7 Bài 5: Đường trung trực của một đoạn thẳng Chân trời sáng tạo hay khác: