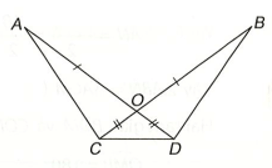
Cho năm điểm A, B, C, D, E như hình vẽ. Biết rằng OA = OB, OC = OD

Cho năm điểm A, B, C, D, E như hình vẽ. Biết rằng OA = OB, OC = OD. Chứng minh rằng:

Giải Vở thực hành Toán 7 Luyện tập chung trang 76, 77, 78

Bài 3 (4.31) trang 76 vở thực hành Toán lớp 7 Tập 1: Cho năm điểm A, B, C, D, E như hình vẽ. Biết rằng OA = OB, OC = OD. Chứng minh rằng:

a) AC = BD;

b) ∆ACD = ∆BDC.

Lời giải:

a) Xét hai tam giác OAC và OBD có:

OA = OB (theo giả thiết).

$\widehat{AOC}=\widehat{BO\text{D}}$ (2 góc đối đỉnh).

OC = OD (theo giả thiết).

Vậy ∆OAC = ∆OBD (c – g – c). Do đó AC = BD (2 cạnh tương ứng).

b) Hai tam giác ACD và BDC có:

AC = BD (chứng minh trên).

CD là cạnh chung;

AD = AO + OD = BO + OC = BC.

Vậy ∆ACD = ∆BDC (c – c – c).