Giải Vở thực hành Toán 7 trang 70 Tập 2 Kết nối tri thức

Với Giải VTH Toán 7 trang 70 Tập 2 trong Bài 32: Quan hệ giữa đường vuông góc và đường xiên Vở thực hành Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 70.

Giải Vở thực hành Toán 7 trang 70 Tập 2 Kết nối tri thức

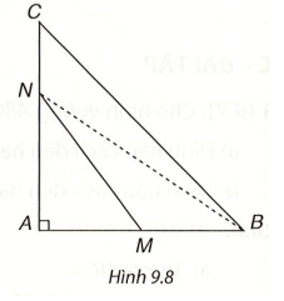
Bài 3 (9.9) trang 70 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.8). Chứng minh rằng MN < BC. (Gợi ý. So sánh MN với NB, NB với BC).

Lời giải:

Tam giác NAM vuông tại A nên $\widehat{AMN}$ là góc nhọn, suy ra $\widehat{NMB}=180°-\widehat{AMN}$ là góc tù. Trong tam giác NMB, góc NMB là lớn nhất nên MN < NB.   (1)

Tương tự, tam giác ABN vuông tại A nên $\widehat{BNA}$ là góc nhọn; suy ra $\widehat{BNC}$ là góc tù. Trong tam giác BCN, góc BNC lớn nhất nên BN < BC. (2)

Từ (1) và (2) ta có MN < BC.

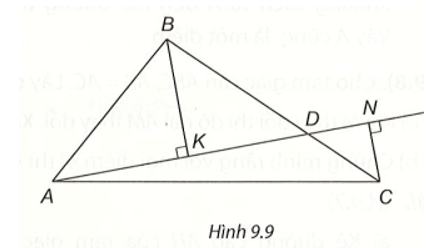
Bài 4 trang 70 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD.

a) So sánh BK, BD.

b) So sánh BK + CN với BC.

c) Chứng minh BK + CN < $\frac{1}{2}$(AB + BC + CA).

Lời giải:

a) Trong tam giác vuông BKD có BD là cạnh huyền nên BK < BD.  (1)

b) Từ (1) suy ra BK + CN < BD + CN.         (2)

Trong tam giác vuông CND có CD là cạnh huyền nên CN < CD,

suy ra BD + CN < BD + CD. (3)

Từ (2) và (3) suy ra BK + CN < BD + CN < BD + CD = BC.

Do đó, BK + CN < BC.   (4)

c) Trong tam giác vuông ABK có AB là cạnh huyền nên BK < AB.     (5)

Trong tam giác vuông CAN có AC là là cạnh huyền nên CN < AC.      (6)

Từ (4), (5) và (6) suy ra (BK + CN) + BK + CN < BC + AB + AC,

hay    2(BK + CN) < AB + BC + CA,

do đó BK + CN < $\frac{1}{2}$(AB + BC + CA).

Lời giải Vở thực hành Toán lớp 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 70 Tập 2