Giải Vở thực hành Toán 7 trang 73 Tập 2 Kết nối tri thức
Với Giải VTH Toán 7 trang 73 Tập 2 trong Bài 33: Quan hệ giữa ba cạnh của một tam giác Vở thực hành Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 73.
Giải Vở thực hành Toán 7 trang 73 Tập 2 Kết nối tri thức
Bài 2 (9.11) trang 73 vở thực hành Toán lớp 7 Tập 2: a) Cho tam giác ABC có AB = 1 cm và BC = 7 cm. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm).
b) Cho tam giác ABC có AB = 2 cm, BC = 6 cm và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm).
Lời giải:
Đặt CA = b (cm).
a) Cạnh bé nhất của tam giác ABC phải có độ dài 1 (cm).
Ta phải có b là số nguyên thỏa mãn:
7 - 1 < b < 7 + 1 hay 6 < b < 8 nên chỉ có b = 7.
b) Theo giả thiết b là số nguyên, b ≤ 6 và theo định lí bất đẳng thức tam giác, b thỏa mãn 6 < 2 + b, tức là b > 4, suy ra b = 5 hoặc b = 6.
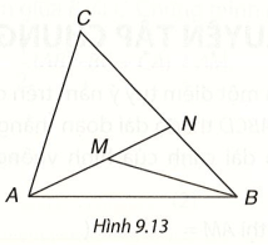
Bài 3 (9.12) trang 73 vở thực hành Toán lớp 7 Tập 2: Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13).
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.
b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB.
c) Chứng minh MA + MB < CA + CB.
Lời giải:
a) Trong tam giác MNB ta có MB < MN + NB, do đó
MA + MB < MA + MN + NB = NA + NB (vì MA + MN = NA).
b) Trong tam giác ACN ta có NA < CA + CN, do đó
NA + NB < CA + CN + NB = CA + CB (vì CN + NB = CB).
c) Từ a) và b) ta có MA + MB < NA + NB,
NA + NB < CA + CB.
Suy ra MA + MB < NA + NB < CA + CB.
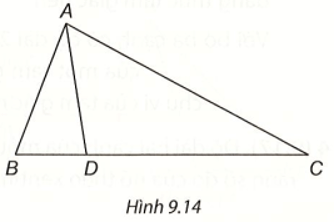
Bài 4 (9.13) trang 73 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh AD nhỏ hơn nửa chu vi tam giác ABC.
Lời giải:
Trong tam giác ABD, ta có AD < AB + BD. (1)
Trong tam giác ACD, ta có AD < AC + CD. (2)
Từ (1) và (2), ta có:
2AD < AB + BD + AC + CD
hay 2AD < AB + AC + (BD + CD) = AB + AC + BC.
Suy ra AD < (AB + AC + BC).
Lời giải Vở thực hành Toán lớp 7 Bài 33: Quan hệ giữa ba cạnh của một tam giác Kết nối tri thức hay khác: