Giải Vở thực hành Toán 7 trang 75 Tập 1 Kết nối tri thức

Với Giải VTH Toán 7 trang 75 Tập 1 trong Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 75.

Giải Vở thực hành Toán 7 trang 75 Tập 1 Kết nối tri thức

Bài 6 (4.28) trang 75 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.

Lời giải:

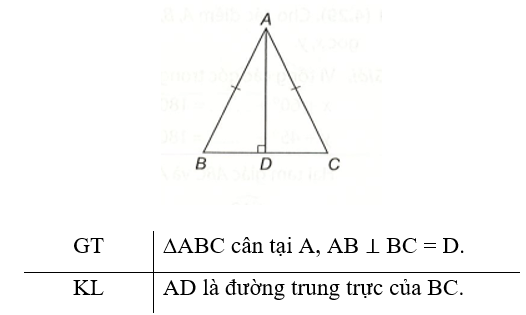
Ta thấy tam giác ABD và tam giác ACD vuông tại D, và có:

AB = AC (∆ABC cân tại A).

AD là cạnh chung.

Vậy ∆ABD = ∆ACD (cạnh góc vuông – cạnh huyền).

Do đó BD = CD (2 cạnh tương ứng). Vậy D là trung điểm của đoạn thẳng BC và do đó AD là đường trung trực của đoạn thẳng BC.

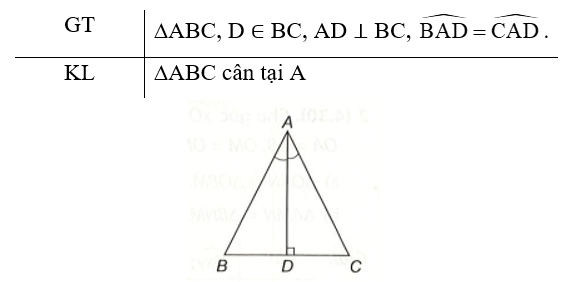
Bài 7 trang 75 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC và điểm D nằm trên cạnh BC sao cho AD vuông góc với BC và AD là phân giác góc BAC. Chứng minh tam giác ABC cân tại A.

Lời giải:

Hai tam giác ADB và ADC cùng vuông tại D và có:

AD là cạnh chung;

$\widehat{BAD}=\widehat{CAD}$ (theo giả thiết).

Vậy ∆ADB = ∆ADC (cạnh góc vuông – góc nhọn). Do đó AB = AC (hai cạnh tương ứng), hay ∆ABC cân tại A.

Bài 8 trang 75 vở thực hành Toán lớp 7 Tập 1: Cho điểm A nằm trên đường trung trực của đoạn thẳng BC sao cho $\widehat{ABC}=60°$. Chứng minh rằng CA = CB.

Lời giải:

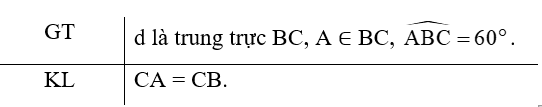
Do A thuộc trung trực BC nên AB = AC, hay ∆ABC cân tại A. Từ đây suy ra $\widehat{ACB}=\widehat{ABC}=60°$. Do tổng các góc trong tam giác ABC bằng 180° nên:

$\widehat{BAC}=180°-\widehat{ABC}-\widehat{ACB}=180°-60°-60°=60°$.

Vậy tam giác ABC có ba góc bằng nhau nên nó là tam giác đều, và do đó CA = CB.

Lời giải Vở thực hành Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 72 Tập 1

• Giải VTH Toán 7 trang 73 Tập 1

• Giải VTH Toán 7 trang 74 Tập 1