Chứng minh rằng nếu nếu tứ giác có hai đường chéo bằng nhau
Giải vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức
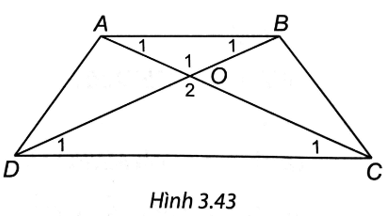
Bài 4 trang 66 vở thực hành Toán 8 Tập 1: Chứng minh rằng nếu nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.43).
Lời giải:
Xét tứ giác ABCD đó có hai đường chéo AC = BD, hai cạnh đối AD = BC.
Hai tam giác ABD và BCA có: cạnh chung AB, AC = BD, AD = BC.
Vậy ∆ABD = ∆BCA (c.c.c).
⇒ (1)
Tương tự, ta có ∆ACD = ∆BDC (c.c.c)
⇒ (2)
Gọi O là giao của hai đường chéo AC và BD thì (hai góc đối đỉnh). (3)
Từ (1), (2), (3), ta có ⇒ AB // CD ⇒ ABCD là hình thang.
Vậy hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Lời giải vở thực hành Toán 8 Bài tập cuối chương 3 hay khác: