Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC
Giải vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức
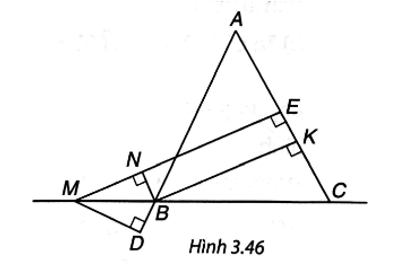
Bài 7 trang 67 vở thực hành Toán 8 Tập 1: Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E, K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống MEvà từ M xuống AB (H.3.46).
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật.
b) BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) tức là BK = ME – MD.
Lời giải:
a) Tứ giác BKEN có ba góc vuông N, E, K nên là hình chữ nhật.
b) Tứ giác BKEN là hình chữ nhật nên NE = BK, BN // EK.
⇒ (hai góc đồng vị). (1)
Ta có (hai góc đối đỉnh). (2)
Theo giả thiết, tam giác ABC cân tại A ⇒ (3).
Từ (1), (2), (3) suy ra
Hai tam giác vuông NBM và DBM có: DB là cạnh chung, (chứng minh trên) nên ∆NBM = ∆DBM (cạnh huyền – góc nhọn) ⇒ MN = MD.
Ta có ME – MD = ME – MN = NE = BK (điều phải chứng minh).
Lời giải vở thực hành Toán 8 Bài tập cuối chương 3 hay khác: