Chứng minh rằng trong một tam giác ABC ta có tanA + tanB + tanC = tanA.tanB.tanC

Ôn tập cuối năm

Bài 11 trang 161 Toán 10: Chứng minh rằng trong một tam giác ABC ta có:

a) tanA + tanB + tanC = tanA.tanB.tanC

b) sin2A + sin2B + sin2C = 4.sinA.sinB.sinC

Trả lời

a) Ta có: A = π - (B + C)

⇒ tanA = -tan(B + C)

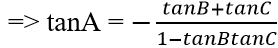
⇒ tanA(1 – tanB.tanC) = -tanB – tanC

⇒ tanA + tanB + tanC = tanA.tanB.tanC (đpcm)

b) Ta có:A + B + C = π

⇒ sin(A + B) = sin(π – C) = sinC

cos(A + B) = cos(π – C) = -cosC

Do đó, 2sin(A + B). cos(A - B) +2sinCcosC

= 2sinC.cos(A - B) + 2sinC[-2cos(A + B)]

= 2sinC(cos(A - B) – cos(A + B))

= 2sinC(-2sinA.sin(-B)

= 4sinAsinBsinC